Quartilabstand
1. Ermittlung der Quartilen
Quartilen entsprechen den Quantilen der Ordnung 1/4 bzw. 3/4. Die untere Quartile (0.25-Quartile) teilt eine der Größe nach geordnete Stichprobenliste so in zwei Teile, dass 25% der Werte unterhalb dieser Quartil liegen und der Rest darüber. Bei der oberen Quartile (0.75-Quartile) wird die Liste so geteilt, dass 75% der Werte unterhalb dieses Grenzwertes liegen.
Beispiel:{1, 4, 5, 6, 7, 8, 8, 10, 10, 11, 12, 13, 14, 14, 15, 15, 15, 16, 17, 17}
Die oben angeführte Stichprobenliste besteht aus 20 Messwerten. Wenn mindestens 25% kleiner oder gleich dem 0.25-Quartil sein müssen, müssen mindestens 5 Werte enthalten sein. Die untere Quartil (0.25-Quartil) ist in diesem Fall 7, da die Werte 1, 4, 5, 6 und 7 kleiner gleich 7 sind. Analog geht man mit der Bildung der 0.75-Quartil vor: Dieser ist 15. Mit 16 würde man nur drei Werte erhalten ( {16, 17, 17} ). Mit 15 erhält man 6 Werte, womit mindestens 25% der oberen Hälfte erfüllt sind.
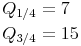
2. Ermittlung des Quartilabstandes
Der Quartilabstand ist widerum nur die Differenz der beiden ermittelten Quartilen und enthält somit 50% der Stichprobenliste, wobei die oberen 25% und die unteren 25% vernachlässigt werden.
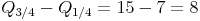
Der Quartilabstand beträgt somit 8.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
D.Schöppe
Mich würde mal Interessieren wo diese "Berchnung" zum Einsatz kommt.
Andreas Mann
Das ist keine Berechnung im klassischen Sinne. Man schaut sich einfach die Probengröße an und nimmt diese mal 0,25 bzw. 0.75 und schaut sich dort das Quartil an. Das dient um die Messverteilung zu veranschaulichen im Bezug zu zum Beispiel Durchschnitt der Werte.
Dr. Ursula Fink
Im angegebenen Beispiel müsste das untere Quartil nach schulbuchmäßiger Berechnungsvorschrift 7,5 (statt 7) sein ...