Vektoralgebra
Ungerichtete / Gerichtete Größen Unterschied
Ungerichtete Größen werden nur durch eine Maßzahl und eine Maßeinheit bestimmt.
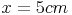
Maßzahl: 5 | Maßeinheit: cm
Man nennt diese Größen Skalare.
Gerichtete Größen geben neben einer Maßzahl auch noch die Richtung oder Orientierung an. Daher kommen gerichtete Größen meist bei Größen der Bewegung vor:
- Geschwindigkeit
- Kräfte
- Feldstärken
- Winkelgeschwindigkeit
Man nennt diese Größen auch Vektoren. Das Wort Vektor stammt vom lateinischen Verb vehere bewegen
Ungerichtete / Gerichtete Größen Beispiele
Hier sehen Sie einige Beispiele um, dies besser unterscheiden zu können:
| Skalar | Vektor |
|---|---|
| Die Körpergröße eines Menschen (z. B. 184 cm) | Der Kurs eines Schiffes (z. B. 20 km Richtung Süd-Osten) |
| Das Alter eines Gebäudes (z. B. 20 Jahre) | Die Verschiebung einer Schachfigur (z. B. 2 Schritte hinauf, 1 Schritt nach rechts) |
| Die Länge eines Orientierungslaufes (z. B. 22 km) | Der Streckenverlauf eines Orientierungslaufes: (z. B. 5,2 km in Richtung 20°; 2,8 km in Richtung 270°; ...) |
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Viktor
Hallo,
ich bin HTL-Schüler und suche zum Thema Mechanik / Kräfte / Physik Beispiele - Hab hier nichts gefunden. Gibt'S da eine andere Rubrik?
Admin
Wir sind bemüht, die Bereiche so umfangreich wie möglich zu gestalten. Leider ist das Spektrum, das wir abdecken wollen enorm groß. Die Vektorrechnung wird dzt. noch recht stiefmütterlich behandelt, denke jedoch, dass du bis spätestens Ende Jänner auch zu diesem Thema Beiträge hier finden wirst.
ahmed mohamed
Kräfte / Physik Beispiele - Hab hier nichts gefunden. Gibt's da eine andere Rubrik?
Kommentar #4 von Admin13.11.10 13:16
Admin
Wir sind bemüht, die Bereiche so umfangreich wie möglich zu gestalten. Leider ist das Spektrum, das wir abdecken wollen enorm groß. Die Vektorrechnung wird dzt. noch recht stiefmütterlich behandelt, denke jedoch, dass du bis spätestens Ende Jänner auch zu diesem Thema Beiträge hier finden wirs