Vektor Grundlagen

Grundlagen der Vektorrechnung: Was ist ein Vektor? Vektorklassen, Ortsvektoren, der Betrag eines Vektors, und vieles mehr
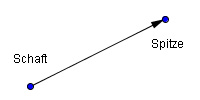
Spitze, Schaft Abb. 1: "Spitze" und "Schaft"

Vektor - Definition

Ein Vektor wird durch drei Angaben festgelegt:

  • Betrag (= Länge)
  • Richtung
  • Orientierung
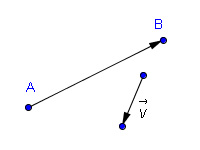Bezeichnung, Vektor, Schreibweise Abb. 2: Vektoren Schreibweise

Vektor - Darstellung

Vektoren werden durch Pfeile abgebildet. Die beiden Enden der Vektoren nennt man "Spitze" und "Schaft" (Siehe Abb. 1).

Gibt der Vektor eine Verschiebung vom Punkt A zum Punkt B an, so wird dieser als

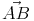
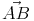
Vektor \vec{{AB}}

bezeichnet.

In allen anderen Fällen symbolisiert man einen Vektor mit einem Kleinbuchstaben und darüber stehendem Pfeil (Siehe auch Abb. 2):

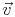
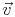
Vektor \vec{v}

Vektoren – Gleichheit

Zwei Vektoren nennt man gleich, wenn diese den gleichen Betrag, die gleiche Richtung und die gleiche Orientierung besitzen.

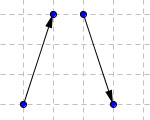Vektor, Gleichheit Abb. 3a
Gleichheit von Vektoren

Beispiel a)

  • Gleicher Betrag
  • Unterschiedliche Richtung
  • Unterschiedliche Orientierung
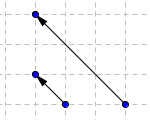Vektor, Gleichheit Abb. 3b
Gleichheit von Vektoren

Beispiel b)

  • Unterschiedlicher Betrag
  • Gleiche Richtung
  • Gleiche Orientierung
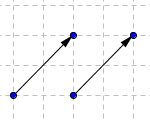Vektor, Gleichheit Abb. 3c
Gleichheit von Vektoren

Beispiel c)

  • Gleicher Betrag
  • Gleiche Richtung
  • Gleiche Orientierung

Diese beiden Vektoren sind gleich

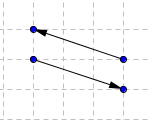Vektor, Gleichheit Abb. 3d
Gleichheit von Vektoren

Beispiel d)

  • Gleicher Betrag
  • Gleiche Richtung
  • Unterschiedliche Orientierung
Kommentar #9750 von Mika 04.03.15 13:36
Mika

Leider gibt es noch nicht viel zu algebra, jedoch hat mir das schon vorhandene weitrr geholfen.
Ich konnte funktionen nicht finden, quadratische lineare und exponential funktionen.

Kommentar verfassen