Betrag des Vektors

Unter dem Betrag eines Vektors versteht man die Länge eines Pfeils. Kennt man die x- und y-Komponente eines Vektors, so kann man daraus die Länge des Vektors ermitteln.

Der Betrag eines Vektors in der Ebene

: Abb. 1: Betrag des Vektors
in der Ebene

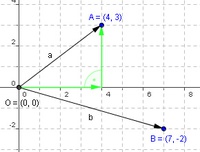
Man erkennt am Beispiel des Vektors a, dass sich dieser aus zwei Verschiebungen zusammensetzen lässt:

4 Schritte nach rechts (= x-Komponente)
3 Schritte hinauf (= y-Komponente)

Da diese beiden Teilvektoren (in der Abbildung grün eingezeichnet) normal zueinander sind, kann man mit Hilfe des Pythagoras die Länge des Vektors ausrechnen:

Beispiele

Betrag des Vektors a:

$|\vec{a}|=\sqrt{a_x^2+a_y^2}$
$|\vec{a}|=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$

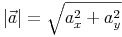
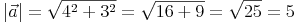
Betrag des Vektors b:

$|\vec{b}|=\sqrt{b_x^2+b_y^2}$
$|\vec{b}|=\sqrt{7^2+(-2)^2}=\sqrt{49+4}=\sqrt{53}=7,2801...\approx7,28$

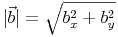
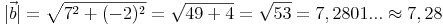
Die Formel zur Berechnung des Betrags in der ebene lautet daher:

$|\vec{v}|=\sqrt{v_x^2+v_y^2}$
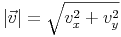
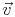$\vec{v}$ ... Vektor
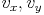$v_x, v_y$ ... x-,y-Komponenten des Vektors

Der Betrag des Vektors im Raum

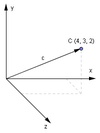
: Abb. 2: Der Betrag des
Vektors im Raum

Wendet man dieses Prinzip auf den Raum an, kann man durch Herleitung folgende Formel ableiten (auf die genaue Herleitung wurde hier verzichtet):

$|\vec{v}|=\sqrt{v_x^2+v_y^2+v_z^2}$

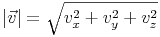
Beispiel

Betrag des Vektors c

$|\vec{c}|=\sqrt{c_x^2+c_y^2+c_z^2}$

$|\vec{c}|=\sqrt{4^2+3^2+2^2}=\sqrt{16+9+4}$

$|\vec{c}|=\sqrt{29}=5,3851\approx5,39$

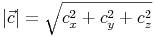
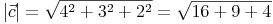
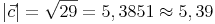
Anmerkung: Der Betrag eines Vektors ist immer eine ungerichtete Größe (Skalar), die nur die Länge des Vektors angibt, aber keinerlei Informationen zu dessen Richtung enthält.

Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema