Ortsvektor

: Abb. 1: Ortsvektoren
in der Ebene

Manchmal ist es notwendig bestimmte Punkte in der Ebene oder im Raum durch gerichtete Größen (Vektoren) abzubilden. Man wählt dazu als Anfangspunkt einfach den Ursprung des Bezugssystems.

Der Ortsvektor in der Ebene

In der Ebene ist der Ursprung des karthesischen Koordinatensystems

$O=\left(\begin{array}{rr}0&0\end{array}\right)$

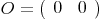
Man gibt also jene Verschiebung an, um vom Ursprung O zu einem bestimmten Punkt zu gelangen.

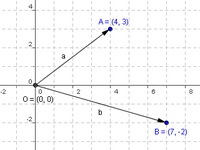
Der Ortsvektor für den Punkt A (4|3) wäre der Vektor

$\vec{a}=\left(\begin{array}{r}4\\3\end{array}\right)$

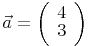
Der Ortsvektor für den Punkt B (7|-2) wäre der Vektor

$\vec{b}=\left(\begin{array}{r}7\\-2\end{array}\right)$

: Abb. 2: Ortsvektor im Raum

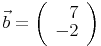
Der Ortsvektor im Raum

Das Prinzip ist im Raum genau das selbe mit dem Unterschied, dass der Ursprung

$O=\left(\begin{array}{rrr}0&0&0\end{array}\right)$

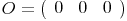
beträgt.

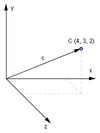
Der Ortsvektor des Punktes C (4|3|2) wäre somit der Vektor

$\vec{c}=\left(\begin{array}{r}4\\3\\2\end{array}\right)$

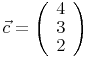
Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema