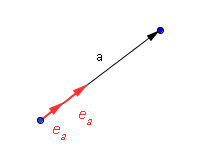
 Abb. 1: Einheitsvektor
Abb. 1: EinheitsvektorEinheitsvektor
Alle Vektoren mit der Länge 1 werden als Einheitsvektoren bezeichnet. Der Einheitsvektor des Vektors a wird oft auch als Vektor 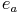 angegeben. Sie erfüllen eine besondere Aufgabe:
angegeben. Sie erfüllen eine besondere Aufgabe:
- Wenn nur die Richtung/Orientierung wichtig ist, kann die Richtung unabhängig von der Länge des Vektors angegeben werden
- Zum Abtragen fix vorgegebener Längen, kann der Einheitsvektor mehrmals aneinander gehängt werden. In der Abbildung sehen Sie zum Beispiel einen Vektor a mit der Länge von 5 Einheiten. Gesucht ist jener Punkt, der vom Startpunkt nach 2 Einheiten erreicht wird. Um diesen zu ermitteln, wird zweimal der Einheitsvektor an den Startpunkt gehängt.
Einheitsvektor - Berechnung
Um den Einheitsvektor eines beliebig langen Vektors zu ermitteln, muss man nur
- die Länge und
- die Komponenten des Vektors (x, y)
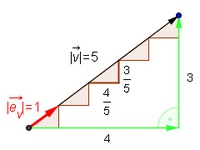
kennen. Betrachtet man die nebenstehende Abbildung, so ist klar, dass ein Vektor mit der Länge 5 sich aus 5 Einheitsvektoren zusammen setzen lässt. Ein Vektor mit der Länge 6 lässt sich aus 6 Einheitsvektoren zusammen setzen, usw.
Um nun den Einheitsvektor berechnen zu können müssen nur die einzelnen Komponenten (x,y) durch den Betrag des Vektors (=Länge) dividiert werden.
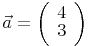
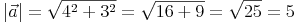
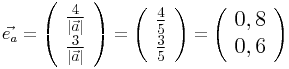
Zur Kontrolle kann man die Länge des Einheitsvektors ausrechnen, die klarerweise 1 ergeben muss:
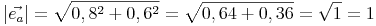
Einheitsvektor Formel - Ebene
Die Formel zur Berechnung des Einheitsvektors lautet somit:
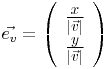
Einheitsvektor Formel - Raum
Die Formel für Einheitsvektoren im Raum lautet:
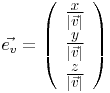
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Peter Wolf
Anregung: gebt doch mal ein einfaches Beispiel aus dem realen Leben für was man den Einheitsvektor braucht.
silverSurfer
Nja, hier geht es um Vektoren. Diese brauchst du in der Geometrie (und somit in der Architektur, 3D-Modellierung/-Visualisierung) in der Physik - überall wo es Vektorfelder gibt (Erdanziehung, Magnetismus) und somit auch in der Meteorologie (noch nie Wetterbericht gesehen?)
Um es mal etwas konkreter zu machen einige Beispiele:
- du möchtest den Winkel zwischen zwei Geraden ermitteln
- du willst den Abstand zwischen einer Geraden und einer Ebene im Raum ermitteln
- Linearkombination
- uvm.
Das was ich auf diesen Seiten gefunden habe, kratzt ja sowieso gerade mal an den Basics der Vektorrechnung. Das ist, wie wenn du in einem Kochkurs fragst, wozu du den Löffel benötigst.
Wenn das "reale Leben" aber natürlich aus Hartz-IV-Empfangen, Konsumieren schwachsinniger Talkshows und dem sonntäglichen Gröhlen in irgendeinem Fußballstadion besteht, dann ist das o.g. Wissen natürlich nicht notwendig ;-) Ich frage mich nur, ob es sinnvoll ist, dass sich die ganze Welt immer am unteren Niveau orientieren muss.
Maksim Rotmann
Auch wenn der Kommentar 3 Jahre alt ist... Sehr geehrter Peter Wolf, haben sie noch nie ein Computer/Smartphone sonstwas spiel gespielt? ^^ Dort kommt man meist auch nicht ohne Vektoren.. und auch nicht ohne Einheitsvektoren aus ^^ zB um bewegungen flüssig darzustellen, animationen zu berechnen, uvm..
Lachhaft
In der Physik wird sehr selten mit Vektoren gerechnet. Vektoren braucht man eigentlich nie auch sogar nicht einmal in der Mechanik. In der Realität rechnet man mit den Beträgen wirkenden Winkel und natürlich für den Fall benötigte Formel.
Stefan
@Lachhaft. Sorry aber dieser Kommentar wirkt dumm. Die Physik ist ein weites Feld. Und unglaublicherweise gibt es sogar Menschen die mit noch komplizierteren Dingen/Methoden als Vektoren rechnen (man glaubt es kaum). Nur weil man es selbst nicht mag oder versteht sollte man nicht behaupten keiner verwendet es.
Giftwicht
Vielleicht ein wenig 'out of topic', aber nach dem Lesen dieses Threads ging mir Folgendes durch den Kopf:
Ich denke, ein jeder hat hier das Recht auf eine respektvolle Antwort; den Lernenden sollte hier doch von den Wissenden geholfen werden (nehm ich mal an). Wenn sich also die Gescheiten untereinander ein Battle liefern wollen, sollten sie es m. E. anderswo tun.
David
Beispiel Ergänzung:
Vektoren spielen beim Programmieren von Videospielen eine große Rolle. Für jede Bewegung im Raum (2D/3D) ist es je nach Spiel und Situation nötig auf Vektoren zurück zu greifen.
Ein einfaches Beispiel im 2D-Raum:
Man steuert eine Figur in x- und y-Richtung (z.B. mit W,A,S,D). Wenn man diese jetzt z.B. diagonal bewegt (W und D gleichzeitig drücken), würde sie sich mit der resultierenden Geschwindigkeit aus x und y, in einem Winkel von 45° nach rechts oben bewegen. Dies würde die Figur jedoch schneller bewegen, da sich beide Geschwindigkeiten, x und y über den Satz des Pythagoras addieren. Hier kommt nun der Einheitsvektor mit Länge=1 ins Spiel und sorgt somit weiterhin für eine gleichmäßige Geschwindigkeit. Die Game-Engines halten dafür Tools im Quellcode bereit, damit man nicht alles von Hand berechnen muss, aber unter der Haube wird mit Vektoren gerechnet.
Sehr vereinfachtes Beispiel aus der Praxis:
playerMove= directionVector.normalized * movementSpeed
Sunny
Danke David für das Beispiel. Mir hat es zum Verständnis geholfen.
bigNemo
von 2017 bis 21 wurde jährlich ein weiterer Kommentar zu dieser Diskussion beigetragen. Schade das diese Kette unterbrochen wurde. Fangen wir 2023 an und führen dies fort. Bitte erst 2024 wieder antworten! Mein Kommentar zu dem Peter Wolf: Vektoren sind Müll die braucht niemand und ich verachte Menschen die so tun als würde man diese tatsächlich irgendwo gebrauchen im praktischen, realen Leben. Ich studiere aber Informatik und brauche diesen Sch**ß für Elektrotechnik (was hat das mit Elektrotechnik zu tun? Keine Ahnung ich checks selber nicht)