Kürzen von Brüchen
Das Kürzen ist das Gegenteil vom Erweitern
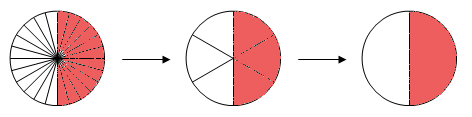
Der Kreis wurde in 24 gleich große Teile unterteilt, 12 davon sind markiert: 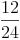
Denselben Wert erhält man, wenn man den Kreis in 6 gleich große Teile unterteilt und 3 davon markiert: 
Denselben Wert erhält man, wenn man den Kreis in 2 gleich große Teile unterteilt und 1 davon markiert: 
Die Brüche 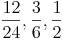 haben noch immer denselben Wert, deshalb gilt:
haben noch immer denselben Wert, deshalb gilt: 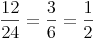
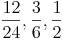 haben noch immer denselben Wert, deshalb gilt:
haben noch immer denselben Wert, deshalb gilt: 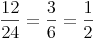
Um rechnerisch von 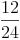 auf
auf  zu kommen, dividiert man Zähler und Nenner durch 4.
zu kommen, dividiert man Zähler und Nenner durch 4.
Um rechnerisch von  auf
auf  zu kommen, dividiert man Zähler und Nenner durch 3.
zu kommen, dividiert man Zähler und Nenner durch 3.
Um rechnerisch von 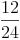 auf
auf  zu kommen, dividiert man Zähler und Nenner durch 12.
zu kommen, dividiert man Zähler und Nenner durch 12.
Kürzen eines Bruches:
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner durch dieselbe Zahl dividiert.
z.B. durch 3 dividiert (= gekürzt) ergibt
durch 3 dividiert (= gekürzt) ergibt  .
.
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner durch dieselbe Zahl dividiert.
z.B.
 durch 3 dividiert (= gekürzt) ergibt
durch 3 dividiert (= gekürzt) ergibt  .
.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
alejandro
Um rechnerisch von 12/24 auf 3/6 zu kommen, dividiert man Zähler und Nenner durch 4
Sophie
Ich fand das ihr diese Mathe seite gut hingekriegt habt-hat mir und meinem sohn sehr geholfen!