Histogramm

Ein Histogramm stellt absolute Häufigkeiten durch Rechtecke dar.

Histogramme

Auf den ersten Blick sehen Histogramme wie Balkendiagramme aus. Der Unterschied liegt hier im Detail: Um ein Histogramm zeichnen zu können, muss man die Werte zuerst in Gruppen zusammenfassen.

Einfache Histogramme stellen Werte gleich breiter Gruppen dar - so wie in folgendem Beispiel.

Beispiel:

30 Personen werden nach ihrem Alter gefragt.

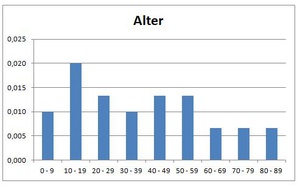
Für ein Histogramm bilden wir Gruppen - in unserem Fall gleich breite Gruppen - z.B. immer 10 Jahre: 0 - 9 Jahre, 10 - 19 Jahre, 20 -29 Jahre, usw.

Folgende Altersangaben wurden gegeben:

11, 27, 31, 29, 83, 75, 52, 48, 71, 17, 16, 9, 12, 3, 55, 51, 45, 32, 38, 28, 62, 68, 41, 59, 5, 11, 14, 25, 44, 88

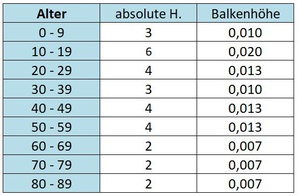
Diese ordnen wir nun in einer Tabelle den richtigen Gruppen zu. So erhalten wir die absolute Häufigkeit.

Für ein Histogramm benötigen wir aber Balkenhöhen, die wir auch einfach zeichnen könnnen. Bei Histogrammen mit unterschiedlichen Gruppenbreiten ist das mit absoluten Zahlen nicht mehr so einfach möglich.

Die Höhe der Balken können wir folgendermaßen berechnen.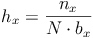

h_x = \frac{n_x}{N \cdot b_x}

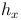h_x steht für die Balkenhöhe

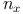n_x steht für die Anzahl der Nennungen dieser Gruppe

N steht für die Gesamtzahl der Nennungen

b_x steht für die Breite dieser Klasse

Z.B. für unsere 1. Klasse von 0 - 9 Jahren: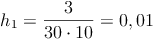

h_1 = \frac{3}{30 \cdot 10} = 0,01

Somit kann man nun ein Histogramm zeichnen.

Das Histogramm:

Ein Histogramm stellt absolute Häufigkeiten durch Rechtecke dar.

Die Höhe der Balken können wir folgendermaßen berechnen.

h_x = \frac{n_x}{N \cdot b_x}

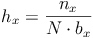
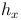h_x steht für die Balkenhöhe

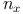n_x steht für die Anzahl der Nennungen dieser Gruppe

N steht für die Gesamtzahl der Nennungen

b_x steht für die Breite dieser Klasse
Kommentar #40416 von jess 19.11.17 12:40
jess

wie kommst du auf die drei in der fuktion?

Kommentar verfassen