Kreisdiagramme

Ein Kreisdiagramm besteht aus einem Kreis, der in mehrere Kreissektoren unterteilt wird, um Teile des Ganzen abzubilden.

Kreisdiagramme

Beispiel:

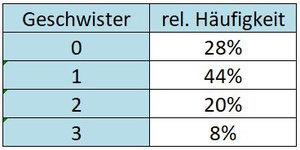
In der 2c werden die 25 Schülerinnen und Schüler nach der Anzahl ihrer Geschwister gefragt.

Der Klassenvorstand rechnet die absoluten Häufigkeiten der Nennungen in die prozentuelle Häufigkeit um:

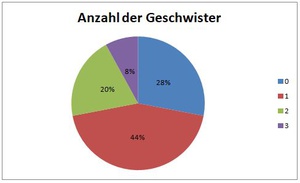
28% der SchülerInnen sind Einzelkinder (haben also keine Geschwister), 44% haben einen Bruder oder eine Schwester, 20% haben zwei Geschwister und 8% haben sogar drei Geschwister.

Kreisdiagramm:

In einem Kreisdiagramm stellt man Teile des Ganzen als Teile des Kreises dar. Die einzelnen Kreissektoren stellen also die Teile des Ganzen anschaulich dar.

Ein ganzer Kreis hat einen Winkel von 360°, ein ganzer Kreis entspricht auch 100 %, daher:

\begin{align} 100\ \% & = 360^\circ \qquad / : 100 \\ 1\ \% & = 3,6^\circ \\ \end{align}

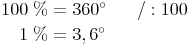
Um die einzelnen Kreissektoren konstruieren zu können, müssen nun die Winkel berechnet werden:

28\ \% = 28 \cdot 3,6^\circ = 100,8^\circ

44\ \% = 44 \cdot 3,6^\circ = 158,4^\circ

20\ \% = 20 \cdot 3,6^\circ = 72^\circ

8\ \% = 8 \cdot 3,6^\circ = 28,8^\circ

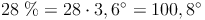
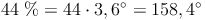
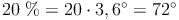
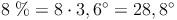
Bei der Konstruktion des Kreisdiagrammes wird mit der Konstruktion eines Kreises begonnen. Anschließend der Radius vom Mittelpunkt z.B. senkrecht nach oben eingezeichnet. Von diesem Radius aus werden nun mit dem Geodreieck die zuvor berechneten Winkel eingezeichnet. Die entsprechenden Kreissektoren können nun färbig hervorgehoben und beschriftet werden.

Anmerkung: Kreisdiagramme lassen sich sehr schnell und einfach mit Tabellenkalkulationsprogrammen (z.B. Microsoft Excel oder Libre Office Calc) konstruieren

Das Kreisdiagramm:

Ein Kreisdiagramm besteht aus einem Kreis, der in mehrere Kreissektoren unterteilt wird, um Teile des Ganzen abzubilden.

Beispiel zur Berechnung der Winkel der Kreissektoren:
55\ \% = 55 \cdot 3,6^\circ = 198^\circ

Kommentar verfassen