Berechnung des vektoriellen Produkts
Hier wird eine einfache Variante zur Berechnung des Kreuzprodukts (vektoriellen Produkts) vorgestellt, für die keine Vorkenntnisse aus dem Bereich der Matrizenrechnung erforderlich sind:
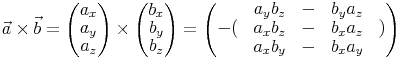
Teilschritte der Berechnung
Da die Formel in ihrer endgültigen Form sehr unübersichtlich zu sein scheint und schwer zu merken ist, stellen wir hier einen einfachen Weg vor, wie man die Teilrechnungen entwickeln kann.
Schritte zur Berechnung einer Zeile:- Um eine Zeile zu berechnen wird exakt diese Zeile abgedeckt
- aus den verbleibenden beiden Zeilen wird überkreuz (wie der Name Kreuzprodukt schon sagt) Produkte gebildet
- und diese Produkte von einander subtrahiert
- Wichtig ist, dass man zuerst von links oben nach rechts unten, dann
- von rechts oben nach links unten multipliziert
- von der kompletten zweiten Zeile wird das Vorzeichen gewechselt
(daher steht diese erneut in einer Klammer mit negativem Vorzeichen)
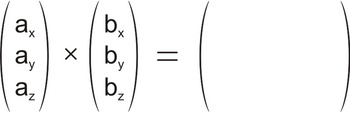 Angabe: Man schreibt die Angabe an und lässt genügend Platz, da die Rechnung recht aufwändig wird
Angabe: Man schreibt die Angabe an und lässt genügend Platz, da die Rechnung recht aufwändig wird Schritt 1: Erste Zeile abdecken, kreuzweise Produkte subtrahieren
Schritt 1: Erste Zeile abdecken, kreuzweise Produkte subtrahieren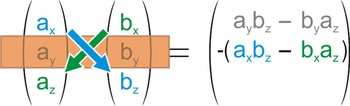 Schritt 2: Zweite Zeile abdecken, kreuzweise Produkte subtrahieren
Schritt 2: Zweite Zeile abdecken, kreuzweise Produkte subtrahieren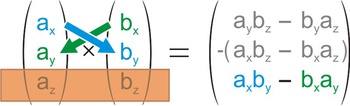 Schritt 3: Dritte Zeile abdecken, kreuzweise Produkte subtrahieren
Schritt 3: Dritte Zeile abdecken, kreuzweise Produkte subtrahieren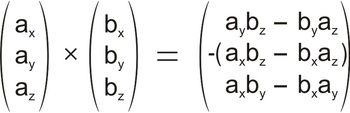 Wichtig: Vorzeichen der zweiten Zeile umkehren!
Wichtig: Vorzeichen der zweiten Zeile umkehren!- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Philipp
Hallo lieber Verfasser!
Vielen Dank für den sehr hilfreichen Artikel! Ich habe nur eine kurze Frage: und zwar, weshalb müssen die Vorzeichen der zweiten Zeile umgetauscht werden?
Vielen Dank und liebe Grüße
Philipp