Direkt proportionale Zuordnungen (y = kx)
Im Kapitel Proportionalität haben wir bereits genau geklärt, worum es sich bei direkt proportionalen Zuordnungen handelt. Die Zusammenfassung davon lesen Sie im Folgenden:
Zuordnungen werden als direkt proportional bezeichnet, wenn eine Größe im geraden Verhältnis zu einer zweiten Größe steht.
Je mehr, desto mehr:
z.B. zum Doppelten der einen Größe gehört das Doppelte der zweiten Größe
zum Fünffachen der einen Größe gehört das Fünffache der zweiten Größe
Je weniger, desto weniger:
z.B.: zur Hälfte der einen gehört die Hälfte der zweiten Größe
zum 5. Teil der einen Größe gehört der 5. Teil der zweiten Größe
Beispiel:
Ein Motorradfahrer fährt auf der Autobahn eine konstante Geschwindigkeit von 120 km/h.
a) Berechnen Sie, wie weit der Motorradfahrer nach 1, 2, 3, 4 und 5 Stunden kommt und stellen Sie hierzu eine einfache Formel auf.
b) Stellen Sie die soeben berechneten Ergebnisse in einer Zurodnungstabelle (Zeit - Weg) dar.
c) Zeichnen Sie ein Schaubild!
a) Tabelle:
Wir brauchen für dieses Beispiel eine Tabelle mit 2 Spalten: In einer Spalte steht die Zeit in Stunden. in der zweiten Spalte der Weg, den der Motorradfahrer in der jeweiligen Anzahl an Stunden zurückgelegt hat.
| Zeit t | Weg s |
|---|---|
| 1 h | 120 km |
| 2 h | 2 . 120 km = 240 km |
| 3 h | 3 . 120 km = 360 km |
| 4 h | 4 . 120 km = 480 km |
| 5 h | 5 . 120 km = 600 km |
b) Formel:
Zeit und Weg verhalten sich direkt proportional zueinander. In 1 Stunde legt der Motorradfahrer 120 km zurück, in 2 Stunden 240 km, in 3 Stunden 360 km, usw. Man multipliziert einfach den zurückgelegten Weg mit der Anzahl der Stunden:
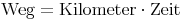
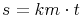
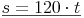
Bei einer gleichförmigen Bewegung stehen Weg und Zeit im selben Verhältnis. Die Zahl 120 bleibt konstant und wird Proportionalitätsfaktor genannt.
c) Schaubild:
Für das Schulbild wählen wir ein Liniendiagramm in einem rechtwinkeligen Koordinatensystem . Auf der x-Achse tragen wir die Zeit in h auf, auf der y-Achse wird der zurückgelegte Weg in km angeschrieben.
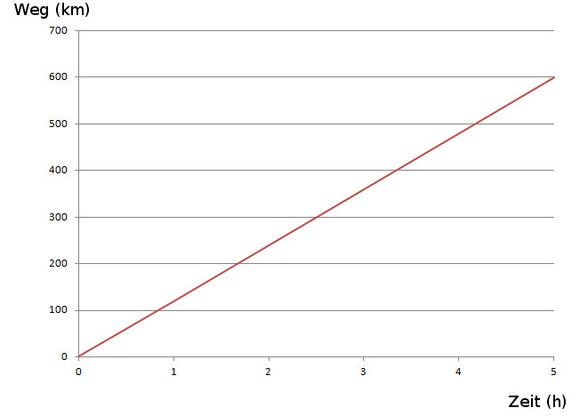 Schaubild
SchaubildDirekt proportionale Zuordnungen werden durch die Formel
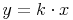 ausgedrückt, wobei k der Proportionalitätsfaktor ist.
ausgedrückt, wobei k der Proportionalitätsfaktor ist.Das Schaubild (bzw. der Graph) einer direkt proportionalen Zuordnung ist eine Halbgerade, die durch den Ursprung verläuft.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar