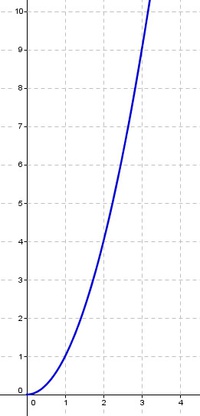
Quadratische Zuordnungen (y = kx²)
Der Graph einer quadratischen Funktion ist ein Teil einer Parabel, die durch den Ursprung verläuft.
Beispiel:
Den Flächeninhalt eines Quadrates berechnet man mit der Formel A=s². Stellen Sie die Abhängigkeit des Flächeninhaltes A von der Seitenlänge s a) in Form einer Tabelle, b) mit einer Formel und c) in einem Schaubild dar.
a) Tabelle:
Wir brauchen für dieses Beispiel eine Tabelle mit 2 Spalten: In einer Spalte steht die Seitenlänge s, in der zweiten Spalte der Flächeninhalt A, die der sich aus der Formel A=s² herleitet.
| Seitenlänge s | Flächeninhalt A |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| ... | ... |
| s | s² |
b) Formel:
Vergrößert man die Seitenlänge auf das 2-fache, 3-fache, 4-fache, ..., so wird der Flächeninhalt 4-mal, 9-mal, 16-mal so groß.
c) Schaubild:
Für das Schaubild zeichnen wir ein kartesisches Koordinatensystem. Für die Zuordnung wird auf der x-Achse die Seitenlänge s angegeben, auf der y-Achse der Flächeninhalt A.
Quadratische ZuordnungenQuadratische Zuordnungen werden durch die Formel
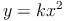ausgedrückt.Das Schaubild (bzw. der Graph) einer quadratischen Zuordnung ist keine Gerade, sondern eine Kurve, die ein Teil einer Parabel ist.
Es gilt:
zum 2-fachen der einen Größe gehört das 4-fache der zweiten Größe,
zum 3-fachen der einen Größe gehört das 9-fache der zweiten Größe,
zum 4-fachen der einen Größe gehört das 16-fache der zweiten Größe, usw.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar