Lineare Zuordnungen (y = kx + d)
Der Graph einer linearen Funktion ist eine Gerade, die nicht durch den Ursprung verläuft.
Beispiel:
Herr Müller fährt auf ein Seminar. Die Fahrtkosten dazu betragen insgesamt 140 Euro. Die Hotelkosten betragen 85 Euro pro Tag.
a) Tabelle:
Wir brauchen für dieses Beispiel eine Tabelle mit 2 Spalten: In einer Spalte steht die Anzahl der Tage, in der zweiten Spalte die Urlaubskosten, die sich aus den Fahrtkosten (einmalig) und den Hotelkosten (täglich) zusammensetzen.
Wie viel muss Herr Müller für das Seminar bezahlen, wenn es 1, 2, 3, 4, 5, 6 bzw. 7 Tage dauert?
| Anzahl der Tage | Urlaubskosten |
|---|---|
| 1 | 140 + 1 . 85 = 225 |
| 2 | 140 + 2 . 85 = 310 |
| 3 | 140 + 3 . 85 = 395 |
| 4 | 140 + 4 . 85 = 480 |
| 5 | 140 + 5 . 85 = 565 |
| 6 | 140 + 6 . 85 = 650 |
| 7 | 140 + 7 . 85 = 735 |
b) Formel:
Die Gesamtkosten setzten sich aus den einmal fälligen Fahrtkosten und den täglich fälligen Hotelkosten zusammen:
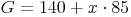
Lineare Funktionen setzten sich immer aus einer festbleibenden Größe (in unserem Fall: Fahrtkosten) und einer veränderlichen Größe (Hotelkosten) zusammen.
c) Schaubild:
Für das Schulbild wählen wir ein Liniendiagramm in einem . Auf der x-Achse tragen wir die Zeit in Tagen auf, auf der y-Achse werden die Urlaubskosten in Euro angeschrieben.
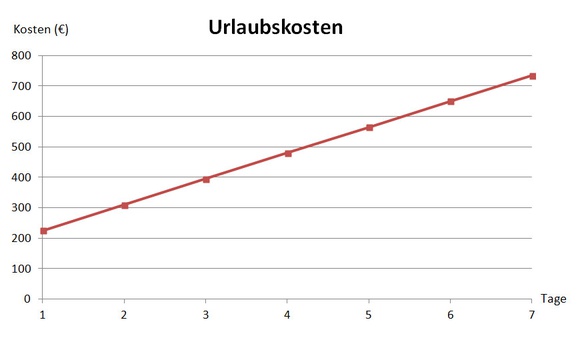Lineare ZuordnungenLineare Zuordnungen werden durch die Formel
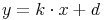ausgedrückt.Bei linearen Zuordnungen ist eine der Größen immer konstant, die andere eine veränderliche Größe.
Das Schaubild (bzw. der Graph) einer linearen Zuordnung ist eine Gerade, die nicht durch den Ursprung verläuft.
Direkt proportionale Zuordnungen sind ein Sonderfall der linearen Zuordnung (weil d = 0).
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Zoe Silber
Der Eintrag hat mir sehr geholfen, aber ich verstehe nicht was d in der Formel ist.
Alina
mir hat der eintrag auch mega gut weiter geholfen....aber ich verstehe auch nich was d in der formel is...:)
Ri Fo
Das d in der Formel stellt den y-Achsenabschnitt dar. Es ist die unveränderliche Größe bei linearen Zuordnungen. Verallgemeinert kann man auch vom Ausgangszustand sprechen. Im oben genannten Beispiel entspricht dies den Fahrtkosten von 140. Egal wie viele Tage er im Hotel übernachtet, die Fahrkosten bleiben gleich hoch.
Igor
D= der anfangswert der gerade
Tom Wegener
ich chec das alles nich