Achsensymmetrische Figuren
Auf dieser Seite beschäftigen wir uns mit Figuren, die bezüglich einer Achse symmetrisch sind.
Beispiel::
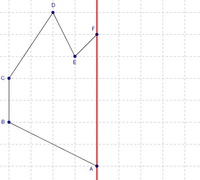
Wir gehen von einer sechseckigen Figur aus, die wir an einer Geraden g (= Spiegelachse) spiegeln wollen.
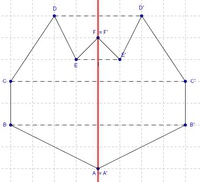
Auf der rechten Seite unserer Spiegelachse entsteht nun eine spiegelverkehrte Kopie unserer Ausgangsfigur.
Mit Hilfe eines Geodreieckes zeichnen wir uns normale Geraden auf die Gerade g durch die einzelnen Eckpunkte unserer Figur ein.
Der Normalabstand (= kürzester Abstand) jedes Eckpunktes von der Gerade g muss auch genau jenem Abstand des gespiegelten Eckpunktes entsprechen.
z.B.:
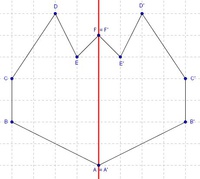
Abschließend können wir die normalen Geraden noch weglöschen, um die Endfigur besser erkennen zu können.
Würde man die Figur nun ausschneiden und entlang der Spiegelachse g falten, so wären beide Hälften deckungsgleich.
Lässt sich eine Figur entlang einer Symmetrieachse (= Spiegelachse, Spiegelgerade) in 2 kongruente (= deckungsgleiche) Teile teilen, so spricht man von einer achsensymmetrischen Figur.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
sara
lol
sara
diese erklärung war sehr hilfreich und hatte alles drin was sie bracht
sara
die erklärung ist sehr hilfreich und man kann danach sofort anfangen zu arbeiten aber man könnte noch mehr bsp hin schreiben
minushiii
Würde gerne wissen wie eine achsensymmetrische Figur entsteht ;)
vali
Übungen währen natürlich auch nicht schlecht... Vielleicht bin ich aber auch einfach nur blind :-)