Verbindung der 4 Grundrechnungsarten (Vorrangregeln)
Auch beim Rechnen mit Brüchen gelten folgende Vorrangregeln:
1. Klammern auflösen (Reihenfolge: runde, eckige, geschwungene, Klammern)
2. Punktrechnungen ausführen ( , :)
, :)
3. Strichrechnungen ausführen (+, -)
Wichtig: Auch innerhalb einer Klammer gilt: Punkt vor Strich!
Beispiel:1. Klammern auflösen (Reihenfolge: runde, eckige, geschwungene, Klammern)
2. Punktrechnungen ausführen (
 , :)
, :)3. Strichrechnungen ausführen (+, -)
Wichtig: Auch innerhalb einer Klammer gilt: Punkt vor Strich!
![\frac {2}{5} + 4 \frac {1}{3} : \left[ \left(2 \frac {1}{2} + \frac {3}{4}\right) \cdot \frac {4}{9} \right] = ? \frac {2}{5} + 4 \frac {1}{3} : \left[ \left(2 \frac {1}{2} + \frac {3}{4}\right) \cdot \frac {4}{9} \right] = ?](/media/formulas/8098f5b46a12ad7fc09f6388036b9a39.png)
1. Gemischte Zahlen in unechte Brüche umwandeln:
![= \frac {2}{5} + \frac {13}{3} : \left[ \left(\frac {5}{2} + \frac {3}{4}\right) \cdot \frac {4}{9} \right] = = \frac {2}{5} + \frac {13}{3} : \left[ \left(\frac {5}{2} + \frac {3}{4}\right) \cdot \frac {4}{9} \right] =](/media/formulas/23f11333ccbba25204db89861adf94bd.png)
2. Runde Klammer ausrechnen (auf den kleinsten gemeinsamen Nenner 4 bringen):
![\begin{align} & = \frac {2}{5} + \frac {13}{3} : \left[ \left(\frac {10}{4} + \frac {3}{4}\right) \cdot \frac {4}{9} \right] = \\ & = \frac {2}{5} + \frac {13}{3} : \left[ \frac {13}{4} \cdot \frac {4}{9} \right] = \\ \end{align} \begin{align} & = \frac {2}{5} + \frac {13}{3} : \left[ \left(\frac {10}{4} + \frac {3}{4}\right) \cdot \frac {4}{9} \right] = \\ & = \frac {2}{5} + \frac {13}{3} : \left[ \frac {13}{4} \cdot \frac {4}{9} \right] = \\ \end{align}](/media/formulas/7431aeaca0de154022168a0715a32f4f.png)
3. Eckige Klammer ausrechnen (die beiden Vierer lassen sich wegkürzen):
![\begin{align} & = \frac {2}{5} + \frac {13}{3} : \left[ \frac {13}{1} \cdot \frac {1}{9} \right] = \\ & = \frac {2}{5} + \frac {13}{3} : \frac {13}{9} = \\ \end{align} \begin{align} & = \frac {2}{5} + \frac {13}{3} : \left[ \frac {13}{1} \cdot \frac {1}{9} \right] = \\ & = \frac {2}{5} + \frac {13}{3} : \frac {13}{9} = \\ \end{align}](/media/formulas/194b28b1ab5f003394d4461ee7e9e5b4.png)
4. Punktrechnungen ausführen (dazu das Divisionszeichen auf ein Malzeichen auswechseln, den Kehrwert des 2. Bruches bilden, 13 mit 13 kürzen, 9 und 3 durch 3 kürzen):
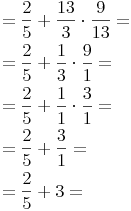
5. Strichrechnungen durchführen:
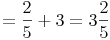
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar