Die prozentuelle Häufigkeit
Beispiel:
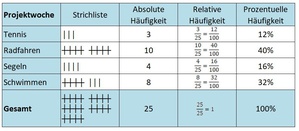
Für die kommende Projektwoche der 4c konnten sich die 25 SchülerInnen für einen Sportschwerpunkt entscheiden. 3 SchülerInnen der Klasse wählten dabei Tennis, 10 SchülerInnen wählten Radfahren, 4 SchülerInnen wählten Segeln und 8 SchülerInnen entschieden sich für Schwimmen.
Strichliste, absolute Häufigkeit und relative Häufigkeit:
Wurden bereits im vorhergehenden Kapitel erklärt.
Prozentuelle Häufigkeit:
Abschließend möchte der Klassenvorstand noch wissen, wie viel Prozent der SchülerInnen sich für die einzelnen Sportarten gemeldet haben - dies ist am aussagekräftigsten.
Da es sich bei einem Bruchstrich um ein Divisionszeichen handelt, können wir die Brüche sehr einfach in eine Dezimalzahl umwandeln und anschließend als Prozentwert ausdrücken.
Eine genauere Anleitung dazu finden Sie im Kapitel Prozentrechnung. 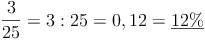
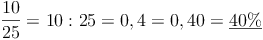
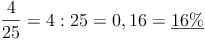
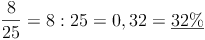
Als prozentuelle Häufigkeit versteht man die relative Häufigkeit in Prozent ausgedrückt:
Man dividiert also die absolute Häufigkeit durch die Gesamtzahl der Beobachtungen.
Beispiel: 2 von 8 Kinder essen am liebsten Pizza:
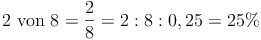
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar