Lineare Gleichungssysteme in 2 Variablen:
Grafisches Lösungsverfahren
Unter einer linearen Gleichung verstehen wir eine Gleichung 1. Grades; das heißt, dass die Variable (z.B. x) nur in der ersten Potenz (ohne Hochzahlen) vorkommt.
Mehrerer solcher linearen Gleichungen bilden ein lineares Gleichungssystem.
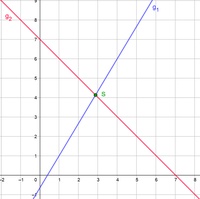
Zeichnet man den Graphen einer linearen Gleichung in ein Koordinatensystem, so entsteht immer eine Gerade.
Die Geraden von linearen Gleichungen schneiden sich meist in 1 Punkt. In Sonderfällen können sie aber auch parallel verlaufen oder identisch sein.
Weitere Informationen:
Treffen sich die Funktionsgraphen (= Geraden) der beiden Gleichungen in genau 1 Punkt, so besteht die Lösungsmenge aus genau einem Zahlenpaar.
Verlaufen die Funktionsgraphen (= Geraden) der beiden Gleichungen parallel zueinander, so ist die Lösungsmenge eine leere Menge.
Sind die Funktionsgraphen (= Geraden) der beiden Gleichungen identisch, so besteht die Lösungsmenge aus unendlich vielen Zahlenpaaren.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar