Lineare Gleichungssysteme in 2 Variablen: Grafisches Lösungsverfahren mit unendlich vielen Lösungen

Sind die Funktionsgraphen (= Geraden) der beiden Gleichungen identisch, so besteht die Lösungsmenge aus unendlich vielen Zahlenpaaren.

Lineare Gleichungssysteme in 2 Variablen: Grafisches Lösungsverfahren mit unendlich vielen Lösungen

Auf dieser Seite zeigen wir Ihnen, wie man das grafische Lösungsverfahren für ein lineares Gleichungssystem mit 2 Gleichungen in 2 Variablen anwendet.

Unser Beispiel wurde so gewählt, dass die Lösungsmenge unendlich viele Lösungen enthält.

Geometrisch bedeutet dies, dass die Funktionsgraphen der beiden linearen Gleichungen (= Geraden) identisch sind und sich somit in unendlich vielen Punkten berühren.

Vorüberlegungen:

Um die beiden linearen Gleichungen mit zwei Variablen in ein Koordinatensystem einzeichnen zu können, müssen sie in ihre Grundform umgewandelt werden:

Grundform der linearen Funktion:

Die Grundform einer linearen Funktion lautet y = kx + d

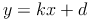
d ist dabei der Normalabstand vom Schnittpunkt der Geraden mit der y-Achse zum Ursprung.

k gibt die Steigung der Geraden an.

Zur Veranschaulichung:

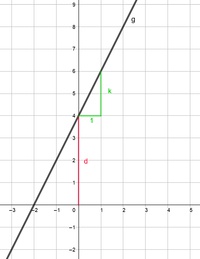
In unserem Beispiel handelt es sich um den Funktionsgraphen der Gleichung y = 2x + 4

Der Normalabstand d vom Schnittpunkt der Geraden mit der y-Achse zum Ursprung beträgt 4 Einheiten.

Nun zeichnet man an diesem Punkt (0 /4) das Steigungsdreieck der Geraden: Dazu misst man eine Einheit waagrecht nach rechts und dann senkrecht nach oben oder unten. Die Länge dieser senkrechten Strecke ist die Steigung k, in unserem Fall 2 Einheiten.

Wir fassen zusammen:

d = 4 und k = 2


Beispiel:


Folgendes Gleichungssystem soll grafisch gelöst werden:

2x + 2y = 16
\underline{3x + 3y = 24}

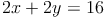
1)
Zuerst müssen die beiden Gleichungen in die Grundform einer linearen Funktion gebracht werden:

Gleichung 1: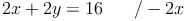

2x + 2y = 16 \qquad / - 2x

Zuerst bringen wir 2x auf die andere Seite: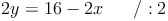
2y = 16 - 2x \qquad / : 2

Anschließend dividieren wir durch 2, um y alleine auf einer Seite stehen zu haben: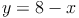
y = 8 - x

Nun bringen wir die Faktoren auf der rechten Seite noch in die Form y = kx + d: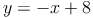
y = -x + 8

Gleichung 2: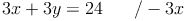

3x + 3y = 24 \qquad / - 3x

Zuerst bringen wir 3x auf die andere Seite: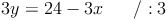
3y = 24 - 3x \qquad / : 3

Anschließend dividieren wir durch 3, um y alleine auf einer Seite stehen zu haben: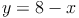
y = 8 - x

Nun bringen wir die Faktoren auf der rechten Seite noch in die Form y = kx + d: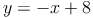
y = -x + 8

2)
Wir können nun erkennen, dass die beiden Gleichungen identisch sind: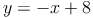

y = -x + 8

3)
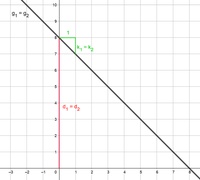
Der Graph der beiden Gleichungen wird nun in ein Koordinatensystem gezeichnet.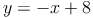

y = -x + 8
y = -1x + 8

k_1 = k_2 = -1

d_1 = d_2 = +8

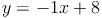
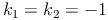
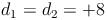
4)
Die beiden Geraden sind identisch. Es gibt also unendlich viele Lösungspunkte.

Somit gilt für die Lösungemenge:

\underline{\mathbb{L} = g}

Lineare Gleichungssysteme in 2 Variablen - 3. Lösungsfall:

Sind die Funktionsgraphen (= Geraden) der beiden Gleichungen identisch, so besteht die Lösungsmenge aus unendlich vielen Zahlenpaaren.

Man schreibt: \mathbb{L} = g}

Kommentar verfassen