Lineare Gleichungssysteme in 2 Variablen: Grafisches Lösungsverfahren mit einer leeren Lösungsmenge

Verlaufen die Funktionsgraphen (= Geraden) der beiden Gleichungen parallel zueinander, so ist die Lösungsmenge eine leere Menge.

Lineare Gleichungssysteme in 2 Variablen: Grafisches Lösungsverfahren mit einer leeren Lösungsmenge

Auf dieser Seite zeigen wir Ihnen, wie man das grafische Lösungsverfahren für ein lineares Gleichungssystem mit 2 Gleichungen in 2 Variablen anwendet.

Unser Beispiel wurde so gewählt, dass die Lösungsmenge leer sein wird.

Geometrisch bedeutet dies, dass die Funktionsgraphen der beiden linearen Gleichungen (= Geraden) parallel zueinander verlaufen und sich somit nicht schneiden.

Vorüberlegungen:

Um die beiden linearen Gleichungen mit zwei Variablen in ein Koordinatensystem einzeichnen zu können, müssen sie in ihre Grundform umgewandelt werden:

Grundform der linearen Funktion:

Die Grundform einer linearen Funktion lautet y = kx + d

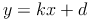
d ist dabei der Normalabstand vom Schnittpunkt der Geraden mit der y-Achse zum Ursprung.

k gibt die Steigung der Geraden an.

Zur Veranschaulichung:

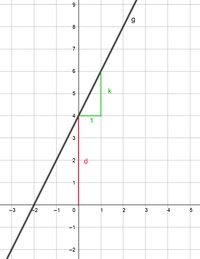
In unserem Beispiel handelt es sich um den Funktionsgraphen der Gleichung y = 2x + 4

Der Normalabstand d vom Schnittpunkt der Geraden mit der y-Achse zum Ursprung beträgt 4 Einheiten.

Nun zeichnet man an diesem Punkt (0 /4) das Steigungsdreieck der Geraden: Dazu misst man eine Einheit waagrecht nach rechts und dann senkrecht nach oben oder unten. Die Länge dieser senkrechten Strecke ist die Steigung k, in unserem Fall 2 Einheiten.

Wir fassen zusammen:

d = 4 und k = 2


Beispiel:


Folgendes Gleichungssystem soll grafisch gelöst werden:

2x + y = 5
\underline{2x + y = 2}

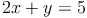
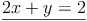
1)
Zuerst müssen die beiden Gleichungen in die Grundform einer linearen Funktion gebracht werden:

Gleichung 1: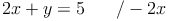

2x + y = 5 \qquad / - 2x

Zuerst bringen wir 2x auf die andere Seite: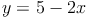
y = 5 - 2x

Nun bringen wir die Faktoren auf der rechten Seite noch in die Form y = kx + d: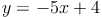
y = -5x + 4

Gleichung 2: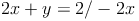

2x + y = 2 \qqad / -2x

Zuerst bringen wir 2x auf die andere Seite: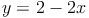
y = 2 - 2x

Nun bringen wir die Faktoren auf der rechten Seite noch in die Form y = kx + d: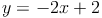
y = -2x + 2

2)
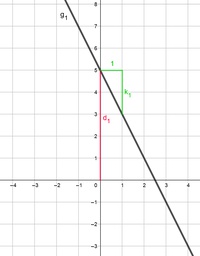
Der Graph der ersten Gleichung wird nun in ein Koordinatensystem gezeichnet.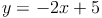

y = -2x + 5

k_1 = -2

d_1 = +5



3)
Der Graph der zweiten Gleichung wird nun in ein Koordinatensystem gezeichnet.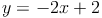

y = -2x + 2

k_2 = -2

d_2 = +2

4)
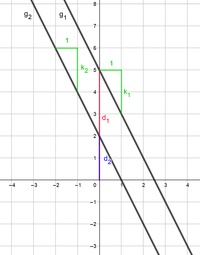
Man kann in der Zeichnug erkennen, dass die beiden Graphen der linearen Gleichungen parallel verlaufen und so einander nicht schneiden.

Für die Lösungemenge gilt daher: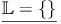

\underline{\mathbb{L} = \{ \}}

Lineare Gleichungssysteme in 2 Variablen - 2. Lösungsfall:

Verlaufen die Funktionsgraphen (= Geraden) der beiden Gleichungen parallel zueinander, so ist die Lösungsmenge eine leere Menge.

Man schreibt: \mathbb{L} = \{ \}

Kommentar verfassen