Einsetzungsverfahren
Das Einsetzungsverfahren ist eine rechnerische Möglichkeit, um ein Gleichungssystem zu lösen.
Beispiel:
Für 2 gleich teure Tablets und eine Schutzhülle zahlt Herr Huber insgesamt 820 Euro. Die Schutzhülle ist um 260 Euro billiger als ein Tablet. Wie viel € kostet ein Tablet und wie viel € kostet die Schutzhülle?
1. Aufstellen des Gleichungssystems:
2 gleich teure Tablets: 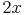
Schutzhülle: 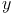
Gesamtpreis: 820 Euro: 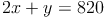
Tablet: 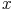
Schutzhülle: 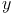
Die Schutzhülle ist um 260 Euro billiger als ein Tablet: 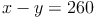
Gleichungssystem: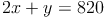
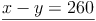
2. Lösen des Gleichungssystems: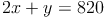
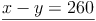
a) Eine der Gleichungen nach einer Variablen auflösen: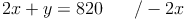
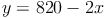
b) Den Term für diese Variable nun in die andere Gleichung einsetzen: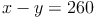
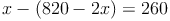
c) Die so entstandene Gleichung mit einer Variablen lösen: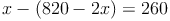
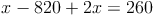
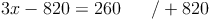
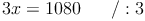
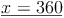
d) Die Lösung in die umgeformte Gleichung einsetzen und diese lösen: 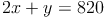
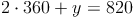
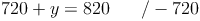

3. Antwort:
Ein Tablet kostet 360 Euro und eine Schutzhülle kostet 100 Euro.
Das Einsetzungsverfahren ist eine rechnerische Möglichkeit, um ein Gleichungssystem zu lösen.
Vorgehensweise:
1) Eine der Gleichungen nach einer Variablen auflösen
2) Den Term für diese Variable nun in die andere Gleichung einsetzen
3) Die so entstandene Gleichung mit einer Variablen lösen
4) Die Lösung in die umgeformte Gleichung einsetzen und diese lösen
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar