Eliminationsverfahren
Das Eliminationssverfahren ist eine rechnerische Möglichkeit, um ein Gleichungssystem zu lösen.
Dabei werden die beiden Gleichungen addiert bzw. subtrahiert, weshalb man oft auch vom Additionsverfahren bzw. Subtraktionsverfahren spricht.
Beispiel:
Für 2 gleich teure Tablets und eine Schutzhülle zahlt Herr Huber insgesamt 820 Euro. Die Schutzhülle ist um 260 Euro billiger als ein Tablet. Wie viel € kostet ein Tablet und wie viel € kostet die Schutzhülle?
1. Aufstellen des Gleichungssystems:
2 gleich teure Tablets: 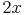
Schutzhülle: 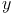
Gesamtpreis: 820 Euro: 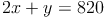
Tablet: 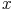
Schutzhülle: 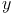
Die Schutzhülle ist um 260 Euro billiger als ein Tablet: 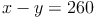
Gleichungssystem: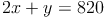
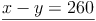
2. Lösen des Gleichungssystems: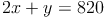
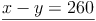
Hat eine Variable in beiden Gleichungen dieselben Koeffizienten, so fällt die Variable beim Addieren bzw. Subtrahieren weg.
In unserem Fall hat die Variable y in beiden Gleichungen den Koeffizienten 1, wobei das positive oder negative Vorzeichen keine Rolle spielen.
a) Somit können wir die Gleichungen addieren:
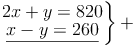
b) Dadurch entsteht folgende neue Gleichung, die wir auch gleich lösen: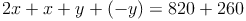
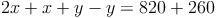
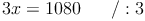
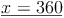
c) Diese Lösung in eine der beiden Gleichungen einsetzen und diese lösen: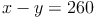

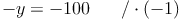
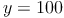
3. Antwort:
Wir fassen zusammen:
Tablet: 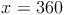
Schutzhülle: 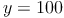
Ein Tablet kostet 360 Euro und eine Schutzhülle kostet 100 Euro.
Das Eliminationsverfahren ist eine rechnerische Möglichkeit, um ein Gleichungssystem zu lösen. Dazu muss eine der beiden Variablen in beiden Gleichungen denselben Koeffizienten haben.
Vorgehensweise:
1) Gegebenfalls eine oder beide Gleichungen multiplizieren, damit eine der beiden Variablen in beiden Gleichungen denselben Koeffizienten hat
2) Die beiden Gleichungen untereinander schreiben und addieren bzw. subtrahieren
3) Die so entstandene Gleichung mit einer Variablen lösen
4) Die Lösung in eine der beiden Ausgangsgleichungen einsetzen und diese lösen
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Hey
Sehr guter Artikel, hat mir sehr weitergeholfen