Exponentialfunktion

Ableitungsfunktionen in der Differentialrechnung: Die Exponentialfunktion

Ableitungsfunktion für Exponentialfunktion

Die Funktion f(x) = ex ist differenzierbar und es gilt:

\begin{align} f(x) & =e^x \\ f'(x) & =e^x \\ \end{align}

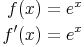
Diese einfache Formel bedarf keiner weiteren Erläuterung. Wichtig ist jedoch, dass weiterhin alle Regeln wie gehabt angewendet werden müssen.

Ableitung von Exponentialfunktionen

Beispiel - Produktregel:

\begin{align} & f(x)=(x^3-2x^2+5x) \cdot e^x \\ & f'(x)=(3x^2-4x+5) \cdot e^x + (x^3-2x^2+5x) \cdot e^x = \\ & = (x^3+x^2+x+5) \cdot e^x \\ \end{align}

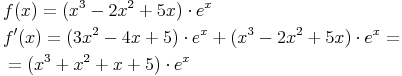
Man beachte, dass hier zwei Funktionen miteinander kombiniert werden und diese nach der Produktregel

f_1(x) \cdot f_2'(x) + f_1'(x) \cdot f_2(x)

abgeleitet werden müssen. f2 und f2' bestehen in diesem Fall aus dem gleichen Term (ex).

Kommentar verfassen