Differentialrechnung - Einführung
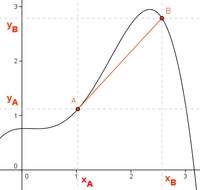
Eine Funktion ist eine geordnete Zuordnung von Wertepaaren (x, f(x)), wobei f(x) der Funktionswert der Funktion f an der Stelle x ist. Um nun die Steigung dieser Funktion zu ermitteln, ist es in der Realität notwendig zwei Messungen zu zwei unterschiedlichen Zeitpunkten vorzunehmen, um anschließend die Veränderung der Funktionswerte ( f(xA), f(xB) ) den Messpunkten (xA, xB) gegenüberzustellen.
Die daraus resultierende Steigung entspricht der Sekante zwischen diesen beiden Punkten A und B. Man erkennt dass dies natürlich weder der Steigung im Punkt A noch der Steigung im Punkt B entspricht.
Mehr dazu finden Sie in der Rubrik Sekantensteigung .
Vom Differenzenquotient zum Differentialquotient
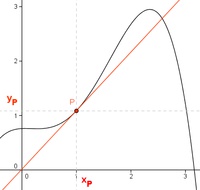
Da für die Angabe einer Steigung zwei Punkte (und somit ein Interval) erforderlich sind, kann die Steigung in einem einzelnen Punkt nicht direkt ermittelt werden. Es ist jedoch möglich einen der beiden Punkte immer näher zum ersten Punkt zu verschieben bis der Abstand unendlich klein wird.
Mit Hilfe der Grenzwertfunktionen kann dies realisiert werden. Genaueres dazu finden Sie unter Tangentensteigung .
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar