Aufstellen der Tangentengleichung
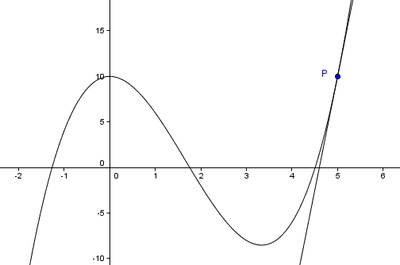Tangente an der Stelle 5Gegeben Sei die Funktion f:
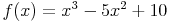
Die erste Ableitung lautet:
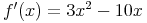
Gesucht ist
- die Steigung an der Stelle 5 und
- die Gleichung jener Tangente, die die Kurve an der Stelle x=5 berührt.
Ermitteln der Steigung
Um die Steigung k an der Stelle x=5 zu ermitteln wird der Wert in die erste Ableitung eingesetzt:
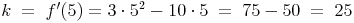
Weiters ist ein Punkt der Tangente erforderlich. Dies ist klarerweise der Berührpunkt P an der Stelle f(5):
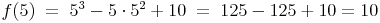
Der Berührpunkt P hat daher die Koordinaten P(5 | 10).
Bekanntlicherweis lässt sich eine Geradengleichung mit gegebener Steigung und einem Punkt aufstellen. Die allgemeine Gleichung lautet:
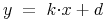
k ... Steigung
d ... Verschiebung entlang der y-Achse
Wir kennen sowohl die Steigung k als auch die Koordinaten eines Punktes. Durch Einsetzen erhält man dadurch:
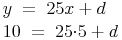
Durch Umformen erhält man:
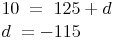
Die endgültige Tangentengleichung für den Funktionswert an der Stelle 5 lautet:
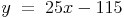
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
sopsie
das half mir nicht weiter
Artur
Danke sehr! Hat geholfen :)
Fabio
Fabio versteht das nicht
Philipp
Vielen Dank, das hier hat es wunderbar erklärt.
Marleen
Lieben Dank, Ausführungen super nachvollziehbar und verständlich!
Nosa
Ich finde es klar
Neerdelerd
Dankeschön war echt hilfreich;)
Pepe
und wie berechne ich jetzt
I: 144 = 995 * k +d
II: 189 = 815 *k +d
Lösung: k = -0,25;
d = 392,75
Hazal
Vielen lieben Dank! Hat mir super beim Nachvollziehen geholfen! Hatte mir ein paar Videos angeschaut, die mich leider nicht weitergebracht haben. Aber jetzt verstehe ich es endlich. Merci. :)
Behemoth
Super! Danke sehr :)
David
oder alternativ:
tau(x) = f(a)+(x-a)*f'(a)
also in diesem Fall:
tau(x) = 10+(x-5)*25 = 25x-115
Sammantha Sarabia
Sehr deutlich geklärt!! Meine bedankung an euch!!! Vielen dank !
Gunther
Meiner Meinung nach ist dieser Beitrag außerordentlich gelungen, er hat mir sehr viel Spaß bereitet und ich freue mich sehr, dass ich diese wunderbare Seite entdecken durfte!:-)
tim
Ja war ganz hilfreich. Man hätte noch näher drauf eingehen können- sonst war es aber gut
Johannes Ger
gute erklaerung ,ich frag mich nur wie ihr die Steigung 25 raus bekommen konntet,habe die x-methode angewannt und f`(x)=1/5x^2 +x rausbekommen,wenn man da fuer x die 5 eingibt kommt auch 10 bei y raus ,wie bilde ich jetzt k?
Lars
Ich berechne es immer so:
1.Schritt: Y-Wert des Punktes berechnen P(5/Y)
f(5)=5^3-5*5^2+10
=125-125+10
=10
P(5/10)
2. Schritt: Jetzt berechnet man die Steigung von P, dazu muss man die x-Koordinate nur in die erste Ableitung einsetzen:
f`(5)=3*5^2-10*5
=75-50
=25
Nun kann man mit der Punktsteigungsform die Tangente berechnen:
Punktsteigungsform:
y = m * ( x - X ) + Y
m ist die Steigung, in diesem Fall 25
X die X-Koordinate von P
Y die Y-Koordinate von P
so ergibt sich:
y = 25 * ( x - 5 ) + 10
= 25x - 125 + 10
= 25x - 115
(Aufpassen: P(X/Y) sind IMMER das Zweite X in der Klammer und das Y nach den Klammer in der Punktsteigungsform [und nicht das erste x vor dem Minus und das y vor dem Gleichzeichen])
Katja
War sehr nachvollziehbar aber trotzdem bin ich bei meiner Gleichung nicht auf das Ergebnis gekommen, welches mein Taschenrechner von mir hören wollte. Bei y=2x^3-4x+1 an x=1 sollte y=2x-3 als tangentengleichung rauskommen und nicht y=2x+7 :D
vici
wir haben so Aufgaben wie:
Bestimme die Gleichung der Tangente t durch den Punkt P.
und gegeben ist:
f(x)=-x^2+3; P(4|f(4))
wie rechnet man das? mich verwirrt, was ich mit diesem Punkt P(4|f(4)) anstellen soll?
mat
Ja und jetzt bestimm mal die Steigung von y = (1-3x)*e^(2x) bei x=1
Steiler oder flacher als 45°
Hannah
Was ist das c in der Tangentengleichung ?