Ableitungsregeln für trigonometrische Funktionen
Hier finden Sie die wichtigsten Ableitungsregeln für trigonometrische Funktionen:
Die Ableitungsregel für die Sinusfunktion lautet:
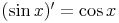
Die Ableitungsregel für die Cosinusfunktion lautet:
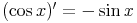
Von diesen beiden lassen sich weitere Funktionen für Tangens und Cotangens ableiten:
Die Ableitungsregel für die Tangensfunktion lautet:
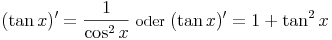
Die Ableitungsregel für die Cotangensfunktion lautet:
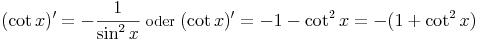
Ableitungsregeln für Kreisfunktionen
Hier finden Sie die wichtigsten Ableitungsregeln für Kreisfunktionen:
Die Ableitungsregel für die Arcussinusfunktion lautet:
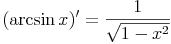
Die Ableitungsregel für die Arcuscosinusfunktion lautet:
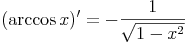
Die Ableitungsregel für die Arcustangensfunktion lautet:
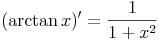
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar