Ableitungsfunktion für Potenzfunktionen
Für Potenzfunktionen dieser Art
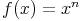
gilt folgende allgemeine Ableitungsfunktion:
Die Ableitung einer Potenzfunktion lautet:
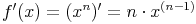
Beispiele zur Potenzfunktion
Die folgenden drei Beispiele zeigen die Anwendung dieser Ableitungsfunktion an sehr einfachen Potenzfunktionen mit positivem Exponenten:
Beispiel 1
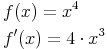
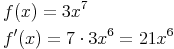
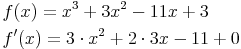
Anmerkung: Man erkennt, dass bei einer Potenzfunktion mit Exponent 1 die Variable wegfällt, da x0=1 gilt.
Die hier vorgestelle Ableitungsfunktion ist aber auch für Potenzfunktionen mit negativem Exponenten gültig:
Beispiel 4
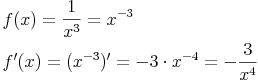
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar