Die Rangordnung der Grundrechnungsarten
Die Reihenfolge, in der man die einzelnen Rechenarten ausführen muss, ist in der Mathematik genau festgelegt.
Rechenarten:
Strichrechnungen: Addition ( + ), Subtraktion ( - )
Punktrechnungen: Multiplikation ( ), Division ( : )
), Division ( : )
Strichrechnungen: Addition ( + ), Subtraktion ( - )
Punktrechnungen: Multiplikation (
 ), Division ( : )
), Division ( : )
Hält man sich nicht an diese Reihenfolge, erhält man unterschiedliche (falsche) Ergebnisse:
Beispiel:
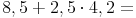
Lösungsweg 1: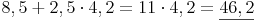
Lösungsweg 2: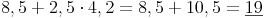
Lösungsweg 1 ist in unserem Beispiel allerdings falsch! Hier haben wir uns nicht an die Rangordnung der Grundrechnungsarten gehalten, die wir Ihnen im Folgenden auflisten werden:
Die Rangordnung der Grundrechnungsarten und Klammern:
1. Klammern auflösen: ( ) , [ ] , { }
2. Hochzahlen berechnen: z.B. ² , ³
3. Punktrechnungen durchführen: , :
, :
4. Strichrechnungen durchführen: + , -
Wichtig: Auch innerhalb der Klammern gilt: Hochzahlen vor Punkt vor Strich!
Beispiel 1:1. Klammern auflösen: ( ) , [ ] , { }
2. Hochzahlen berechnen: z.B. ² , ³
3. Punktrechnungen durchführen:
 , :
, :4. Strichrechnungen durchführen: + , -
Wichtig: Auch innerhalb der Klammern gilt: Hochzahlen vor Punkt vor Strich!
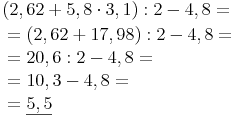
![\begin{align} & [(14,4 + 3,7 \cdot 6) + 28,8 : 2,5] - 5,1 \cdot 7,2 = \\ & = [(14,4 + 22,2) + 28,8 : 2,5] - 5,1 \cdot 7,2 = \\ & = [36,6 + 28,8 : 2,5] - 5,1 \cdot 7,2 = \\ & = [36,6 + 11,52] - 5,1 \cdot 7,2 = \\ & = 48,12 - 5,1 \cdot 7,2 = \\ & = 48,12 - 36,72 = \\ & = \underline{11,4} \\ \end{align} \begin{align} & [(14,4 + 3,7 \cdot 6) + 28,8 : 2,5] - 5,1 \cdot 7,2 = \\ & = [(14,4 + 22,2) + 28,8 : 2,5] - 5,1 \cdot 7,2 = \\ & = [36,6 + 28,8 : 2,5] - 5,1 \cdot 7,2 = \\ & = [36,6 + 11,52] - 5,1 \cdot 7,2 = \\ & = 48,12 - 5,1 \cdot 7,2 = \\ & = 48,12 - 36,72 = \\ & = \underline{11,4} \\ \end{align}](/media/formulas/3f13c63ec0a895c3e33c81afb3de7d33.png)
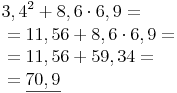
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar