Dekadische Einheiten als Zehnerpotenzen
Potenzen mit der Grundzahl 10 werden Zehnerpotenzen genannt.
Beispiel:Potenzieren Sie die Zahl 10 mit den Hochzahlen 1, 2, 3, 4, 5 und 6!
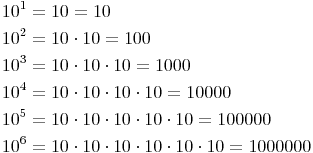
Vergleichen Sie nun die Angaben mit den Ergebnissen.
Sie können erkennen, dass die Anzahl der Nullen im Ergebnis identisch mit der Hochzahl ist.
Einfache Zehnerpotenzen können Sie also auch ohne Taschenrechner lösen. Schreiben Sie im Ergebnis eine 1 und danach so viele Nullen wie Ihnen die Hochzahl sagt.
z.B.: 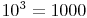
 = zehn
= zehn
 = hundert
= hundert
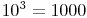 = tausend
= tausend
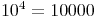 = zehntausend
= zehntausend
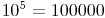 = hunderttausend
= hunderttausend
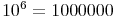 = 1 Million
= 1 Million
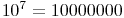 = 10 Millionen
= 10 Millionen
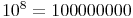 = 100 Millionen
= 100 Millionen
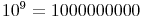 = 1 Milliarde
= 1 Milliarde
Haben Potenzen die Grundzahl 10, so werden sie Zehnerpotenzen genannt.
Die Hochzahl gibt die Anzahl der Nullen im Ergebnis an!
z.B.:
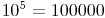
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar