Potenzieren von negativen Zahlen
Aufgabe:Potenzieren Sie die Zahl (-2) der Reihe nach - beginnend mit 1, endend mit 8!
Verwenden Sie dazu am Besten einen Taschenrechner und versuchen Sie, anhand der Ergebnisse eine Regelmäßigkeit herauszulesen.
Durchführung:
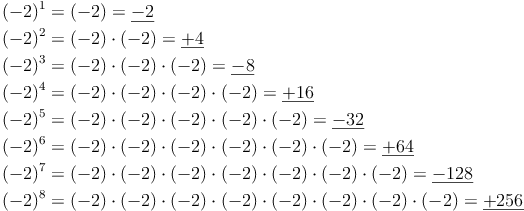
Wie Sie erkennen können, wechseln sich positive und negative Ergebnisse ab.
Handelt es sich um eine gerade Hochzahl, so ist das Ergebnis positiv.
Handelt es sich um eine ungerade Hochzahl, so ist das Ergebnis negativ.
Potenzieren von negativen Zahlen:
Potenzen mit einer negativen Grundzahl (Basis) sind positiv, wenn die Hochzahl gerade ist.
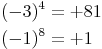
Potenzen mit einer negativen Grundzahl (Basis) sind negativ, wenn die Hochzahl ungerade ist.
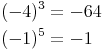
Potenzen mit einer negativen Grundzahl (Basis) sind positiv, wenn die Hochzahl gerade ist.
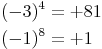
Potenzen mit einer negativen Grundzahl (Basis) sind negativ, wenn die Hochzahl ungerade ist.
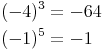
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
ta
super tipp hat mir 1 gegeben