Nicht alle Rechnungen sind in der Menge der ganzen Zahlen lösbar.
Additionen, Subtraktionen und Multiplikationen von ganzen Zahlen führen auf jedem Fall wieder zu einer ganzen Zahl.
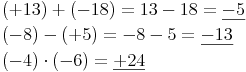
Einzig die Division von ganzen Zahlen ist in der Menge der ganzen Zahlen nicht immer bzw. im Normalfall nicht lösbar.
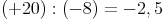
Damit auch wirklich jede Division (Divisor 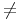 0) ausführbar ist, müssen wir mit den positiven und negativen Dezimalzahlen arbeiten. Diese erweiterte Zahlenmenge nennen wir die Menge der rationalen Zahlen. Sie wird mit einem
0) ausführbar ist, müssen wir mit den positiven und negativen Dezimalzahlen arbeiten. Diese erweiterte Zahlenmenge nennen wir die Menge der rationalen Zahlen. Sie wird mit einem 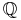 (Q mit 2 senkrechten Linien in der Mitte) abgekürzt.
(Q mit 2 senkrechten Linien in der Mitte) abgekürzt.
Die Abkürzung  steht für Quotient. Rationale Zahlen sind als der Ergebnis einer Division.
steht für Quotient. Rationale Zahlen sind als der Ergebnis einer Division.
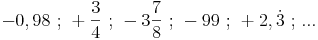
Allgemein lässt sich jede Zahl als Bruch anschreiben: 
Für a und b lässt sich jede beliebige ganze Zahl einsetzen. Eine Division durch 0 ist allerdings nicht durchführbar, daher darf b zwar jede beliebige ganze Zahl sein, nicht aber 0.
Mathematisch geschrieben: 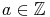 ,
, 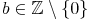
Die Menge der rationalen Zahlen besteht aus der Menge der negativen rationalen Zahlen (
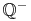 ), der Zahl Null (0) und der Menge der positiven rationalen Zahlen (
), der Zahl Null (0) und der Menge der positiven rationalen Zahlen (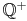 ).
).z.B.:
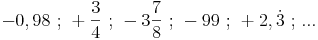
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar