Herausheben gemeinsamer Faktoren
Im Kapitel "Multiplizieren von Summen und Differenzen " haben wir das Distributivgesetz angewendet:
Multiplizieren von Summen und Differenzen:
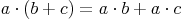
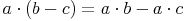
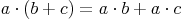
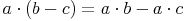
Drehen wir diese Formel(n) nun um, können wir Summen bzw. Differenzen, die gemeinsame Faktoren enthalten, in Produkte umwandeln: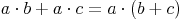
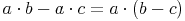
Beispiel 1: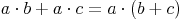
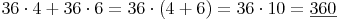
Beispiel 2: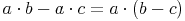
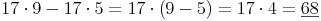
Herausheben gemeinsamer Faktoren:
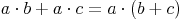
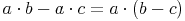
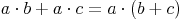
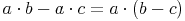
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
???
Tolle Seite...