Mit Hilfe der Ähnlichkeit kann man Strecken in bestimmten Verhältnissen teilen. Hier zeigen wir Ihnen, wie man den dazu benötigten Teilungspunkt konstruktiv ermittelt.
Teilungspunkt 1
Teilungspunkt 2
Teilungspunkt 3
Teilungspunkt 4
Teilungspunkt 5Beispiel:
Teilen Sie die Strecke AB = 10 cm im Verhältnis 4:3!
Schritt 1:
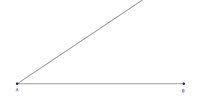
Konstruieren Sie die Strecke AB = 10 cm.
Schritt 2:
Konstruieren Sie vom Punkt A aus einen Strahl im beliebigen Winkel.
Schritt 3:
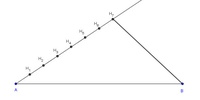
Verhältnis 4:3 --> wir müssen die Strecke in 4 + 3 = 7 gleich große Teile teilen.
Schlagen Sie daher mit Hilfe des Zirkels einen beliebigen Abstand 7 Mal auf dem Strahl ab. Es entstehen die Hilfspunkte H_1 bis H_7.
Schritt 4:
Verbinden Sie den letzten Punkt (H_7) mit dem Endpunkt der Strecke (B).
Schritt 5:
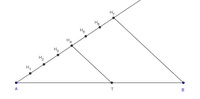
Konstruieren Sie abschließend eine parallele Strecke zu der eben konstruierten Strecke durch den Punkt H_4.
Der so entstandene Teilungspunkt T teilt die Strecke nun in 4 zu 3 Teile.
Recnerische Kontrolle: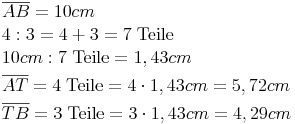
Strecken lassen sich durch die Ähnlichkeit in bestimmten Verhältnissen teilen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
zülal
ok es ist eh nicht soo schlecht beschrieben aber irgendwie kompliziert.und wieviel grad muss man überhaupt dazu messen???
Laurin
Dankeeeee schreibe morgen mathe und hatte keine ahnung wie das nochmal ging, echt super erklärt, war nämlich der letzte punkt auf meiner Liste den ich noch nicht zu 100% verstanden hatte.
LG