b-c-Gamma

Konstruktion eines Dreiecks, bei dem die Seiten b und c sowie der der größeren Seite (= c) gegenüberliegende Winkel (= Gamma) gegeben sind.

Dreieckskonstruktion nach dem SSW-Satz

geg.: Dreieck:

\begin{align} & c = 10\ cm \\ & b = 6\ cm \\ & \gamma = 65^\circ \\ \end{align}

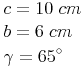
ges.: Konstruktion

Schritt 1: Skizze

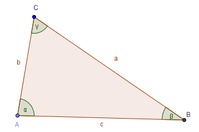
Zeichnen Sie zuerst eine Skizze des Dreiecks und beschriften Sie dieses vollständig (Seiten, Eckpunkte, Winkel).

Die gegebenen Bestimmungsstücke werden nun färbig markiert, um nachher die Konstruktion einfacher durchführen zu können.

Schritt 2: Konstruktion der Seite b

Beginnen Sie mit der Konstruktion der Seite b =6 cm, welche die Eckpunkte A und C verbindet.

Tipp: Legen Sie die Seite b in etwa so wie in ihrer Skizze.

Beschriften Sie die gezeichnete Seite sowie die beiden Eckpunkte.

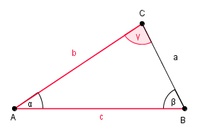
Schritt 3: Konstruktion des Winkels 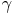\gamma

Aus der Skizze kann man erkennen, dass sich der Winkel 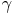\gamma beim Eckpunkt C befindet.

Konstruieren Sie deshalb mit Hilfe des Geodreiecks den Winkel 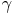\gamma = 65° und beschriften Sie diesen auch gleich.

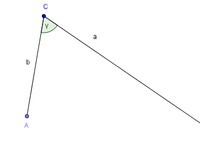
Schritt 4: Konstruktion der Seite c

Aus der Skizze kann man erkennen, dass die Seite c vom Eckpunkt A ausgeht und diesen mit dem Eckpunkt B verbindet.

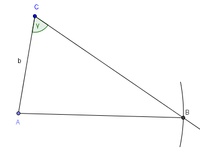
Nachdem wir bereits den Winkel 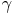\gamma gezeichnet haben und so mit einer Hilfslinie die Lage der Seite a angedeutet haben, müssen wir nun c = 10 cm in den Zirkel nehmen, im Eckpunkt A einstechen und auf dieser Hilfslinie abschlagen.

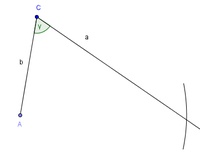
Schritt 5: Der Eckpunkt B

Aus der Skizze kann man erkennen, dass der Schnittpunkt der Hilfsgeraden mit unserem Kreisbogen der Eckpunkt B ist.

Markieren Sie diesen Punkt und beschriften sie ihn auch gleich.

Schritt 6: Beschriftung

Beschriften Sie zuletzt alle Eckpunkte, Seiten und Winkel des Dreiecks.

Ziehen Sie die Seiten mit einem weichen Bleistift oder einem Buntstift nach, um das Dreieck klar von den Hilfslinien abzuheben.

Kommentar #40924 von benjamin 31.03.18 14:46
benjamin

es half mir sehr ein dreieck und vieles mehr zu konstruiren

Kommentar verfassen