Die Winkelsymmetrale (= Winkelhalbierende)
Beispiel:
Konstruieren Sie den Winkel  = 53° und halbieren Sie diesen Winkel!
= 53° und halbieren Sie diesen Winkel!
Am genauesten kann man einen Winkel mit Hilfe der Winkelsymmetrale halbieren. Dazu benötigen wir zuerst einen Zirkel, danach auch ein Geodreieck.
Hier eine Anleitung dazu:
Schritt 1: Winkel konstruieren
Wir konstruieren den Winkel  = 53° und zeichnen vom Scheitelpunkt (S) einen Kreisbogen um die beiden Winkelschenkel. Dabei entstehen die Punkte A und B.
= 53° und zeichnen vom Scheitelpunkt (S) einen Kreisbogen um die beiden Winkelschenkel. Dabei entstehen die Punkte A und B.
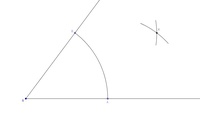
Schritt 2: Kreisbogen von A aus
Wir stechen mit dem Zirkel im Punkt A ein, spannen ihn weiter als der Abstand 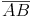 beträgt und schlagen einen Kreisbogen ab.
beträgt und schlagen einen Kreisbogen ab.
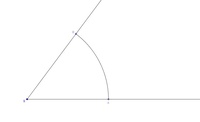
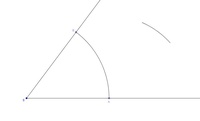
Schritt 3: Kreisbogen von B aus
Wir stechen nun im Punkt B ein und schlagen denselben Radius wie vorher vom Punkt A nun vom Punkt B aus ab.
Unser nun entstandener Kreisbogen muss den anderen Kreisbogen schneiden.
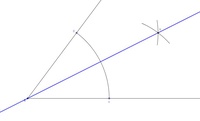
Schritt 4: Winkelsymmetrale
Abschließend verbinden wir nun den soeben entstandenen Punkt (X) mit dem Scheitelpunkt (S). Diese gerade nennt man Winkelsymmetrale des Winkels  .
.
Die Winkelsymmetrale halbiert den Winkel  .
.
Die Winkelsymmetrale
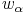 eines Winkels
eines Winkels  halbiert den Winkel
halbiert den Winkel  . Jeder Punkt der Winkelsymmetrale hat von den beiden Winkelschenkeln denselben Normalabstand!
. Jeder Punkt der Winkelsymmetrale hat von den beiden Winkelschenkeln denselben Normalabstand!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
bekim
was ist eigentlich der unterschied der winkelsymetrale und der streckensymetrale
Erich Hnilica, BEd
Die Winkelsymmetrale halbiert einen Winkel.
Die Streckensymmetrale halbiert eine Strecke.
liona
Wie zeichnet man eigentlich eine Streckensymmetrale ?
Alexander
Es hat mir wirklich geholfen weil morgen habe ich Schularbeit. Zum Glück gibt es das Mathe Lexikon. Jetzt bin ich Perfekt vorbereitet
Alexander
Der Unterschied ist nur das Die WS ein Winkel ist und SS eine Strecke
Alexander
Ich hatte in Mathe mich um zwei Noten verbessert. Es half mir so viel. Das wAR MEIN LETZTER KOMMENTAR und ich hoffe es wird euch auch so viel helfen wie mir
ayas
es hilft zwar aber nicht genug
Christian
Wie Hängt die Genauigkeit der Konstruktion vom Radius des Kreisbogens ab ? Führt ein größerer Radius zu höherer Genauigkeit, oder ist das Gegenteil der Fall? Hat die Größe des Radiuses keinen Einfluss auf die Genauigkeit der Konstruktion... ?
Ludwig Plasser
Ich habe sowieso nur 1 und 2