Allgemeines über das kartesische Koordinatensystem
Ein kartesisches (rechtwinkliges) Koordinatensystem besteht aus zwei Geraden, die aufeinander normal stehen.
Die horizontal liegende Gerade wird als x-Achse oder auch als Abszisse (vom lateinischen Wort abscisus = abgebrochen) bzw. als 1. Koordinatenachse bezeichnet.
Die senkrecht liegende Gerade wird als y-Achse oder auch als Ordinate (vom lateinischen Wort ordinatus = geordnet) bzw. als 2. Koordinatenachse bezeichnet.
Normalerweise werden auf beiden Achsen die gleichen Längeneinheiten gewählt.
Jener Punkt, in dem sich die beiden Achsen schneiden wird als Ursprung oder auch als Nullpunkt bezeichnet.
Jeder Punkt im Koordinatensystem ist durch seine Lage eindeutig zu bestimmen. Angegeben wird ein Punkt durch ein Zahlenpaar, welches den Abstand zu den beiden Achsen angibt:
P ( x / y )Beispiel:
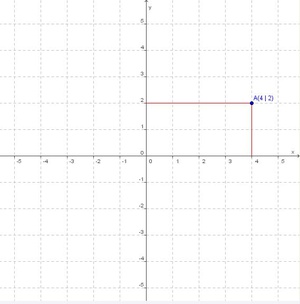
A ( 4 / 2 )
Die Orientierung beginnt immer im Ursprung.
4 ist der Abstand des Punktes A vom Ursprung auf der x-Achse.
2 ist der Abstand des Punktes A von der x-Achse.
Vergleichen kann man es mit einer Wanderung auf einen Berg. Man startet im Ursprung, wandert zuerst in der Ebene zum Berg hin (x-Achse) und erst danach kann man den Berg erklimmen (y-Achse).
Der umgekehrte Weg ist nicht möglich!
Das rechtwinklige Koordinatensystem wird durch zwei Geraden gebildet.
Die waagrechte Gerade wird als x-Achse (Abszisse), die senkrechte Gerade als y-Achse (Ordinate) bezeichnet.
Den Schnittpunkt der beiden Achsen nennt man Ursprung (Nullpunkt).
Jeder Punkt im Koordinatensystem lässt sich als Zahlenpaar in der Form P ( x / y ) darstellen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar