Kartesisches Koordinatensystem: Punkte an der x-Achse spiegeln

Beim Spiegeln von Punkten an der x-Achse ändert sich nur die y-Koordinate des zu spiegelndes Punktes.

Punkte an der x-Achse spiegeln

Beispiel:

Zeichne ein kartesisches (rechtwinkeliges) Koordinatensystem und spiegle die folgenden Punkte an der x-Achse (Abszissenachse):

A ( 3 / 2 )

B ( -1 / -3 )

C ( -4 / 0 )

Schritt 1: Konstruktion des kartesischen Koordinatensystems

Wir zeichnen die beiden Achsen des Koordinatensystem und beschriften diese.

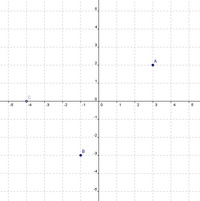
Schritt 2: Punkte in das Koordinatensystem einzeichnen

Die Punkte A, B und C werden in das Koordinatensystem eingetragen.

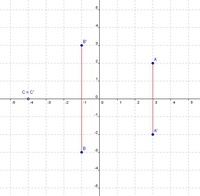
Schritt 3:Spiegelung der Punkte

Nachdem die x-Achse die Spiegelachse unserer Punkte sein soll, müssen die gespiegelten Punkte auf der anderen Seite der x-Achse liegen und genau denselben Abstand von der x-Achse haben wie die Ausgangspunkte.

Beim Spiegeln der Punkte an der x-Achse ändert sich also nur das Vorzeichen der y-Koordinate:

A ( 3 / 2 ) --> A' ( 3 / -2 )

B ( -1 / -3 ) --> B' ( -1 / 3 )

C ( -4 / 0 ) --> C' ( -4 / 0 )

Aus negativen Vorzeichen (-) der y-Koordinate werden also positive Vorzeichen (+) und umgekehrt. Liegt der zu spiegelnde Punkt auf der Spiegelachse selbst (y-Koordinate = 0), so bleibt er gleich.

Spiegeln von Punkten an der x-Achse

Beim Spiegeln von Punkten an der x-Achse ändert sich nur die y-Koordinate des zu spiegelndes Punktes:
X ( x / y ) --> X' ( x / -y )

Beispiele:
A ( -5 / -4 ) --> A' ( -5 / +4 ) oder B ( 6 / 7 ) --> B' ( 6 / -7 )

Kommentar verfassen