Umkehraufgaben: Bruchteile berechnen
Zur Erinnerung:
Bruchteile von Größen:
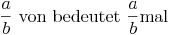
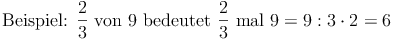
Dies bedeutet: zuerst durch 3 dividieren, dann mit 2 multiplizieren!
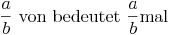
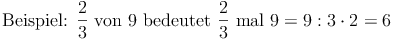
Dies bedeutet: zuerst durch 3 dividieren, dann mit 2 multiplizieren!
Beispiel:
In einem Kirchenchor sind von den insgesamt 28 Mitgliedern 7 Männer.
7 von 28 bedeutet: 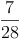
Diesen Bruch können wir noch kürzen, und zwar durch 7: 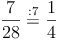
Antwort: der Mitglieder des Kirchenchores sind Männer.
der Mitglieder des Kirchenchores sind Männer.
Erweiterung:
Der Rest der Mitglieder des Kirchenchores sind demnach Frauen.
Alle Mitglieder: 
Männer: 
Frauen: 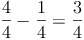
Demnach sind  der Mitglieder des Kirchenchores Frauen.
der Mitglieder des Kirchenchores Frauen.
Umkehraufgaben: Bruchteile berechnen:
Kennt man den Gesamtwert und den Wert eines Teiles und möchte den Bruchteil dieses Teiles berechnen, so bildet man folgenden Bruch:
Den Wert eines Teiles schreibt man in den Zähler, den Gesamtwert schreibt man in den Nenner.
Beispiel: 4 von 15 Kindern haben blonde Haare: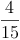
Kennt man den Gesamtwert und den Wert eines Teiles und möchte den Bruchteil dieses Teiles berechnen, so bildet man folgenden Bruch:
Den Wert eines Teiles schreibt man in den Zähler, den Gesamtwert schreibt man in den Nenner.
Beispiel: 4 von 15 Kindern haben blonde Haare:
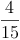
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar