Das Maß für die Menge von Daten ist die Datenmenge.
Das Bit
Die kleinste Einheit ist das Bit. Hierbei handelt es sich um eine binäre Ziffer (siehe auch Binäres Zahlensystem ). Diese Ziffer kann die Werte "0" oder "1" enthalten. Mit der Datenmenge von einem Bit können somit Informationen der folgenden Art übermittelt werden:
- In einer Kundenliste kann zum Beispiel die Information hinterlegt werden, ob der jeweilige Kunde einen Newsletter erhalten möchte (=1) oder nicht (=0)
- In einem redaktionellen CMS-System kann eine Datenmenge von einem Bit entscheiden, ob eine Seite veröffentlicht ist (=1) oder nicht (=0)
- In einem elektronischen Steuerungssystem kann ein Bit die Information liefern, ob ein bestimmtes Teilsystem unter Strom steht oder nicht
Verkettung von mehreren Bits
Da die Welt nun mal nicht nur aus Schwarz und Weiß besteht, und meist mehrere Zustände abgedeckt werden müssen, können durch mehrere Bits auch weitere Zustände abgedeckt werden. Die Anzahl der möglichen Werte kann dabei leicht mit folgender Formel berechnet werden:
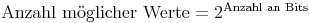
Beispiel Kartenspiel:
Um bei einem Kartenspiel die Information des Blattes (Herz, Karo, Pik, Kreuz) abzubilden, sind zum Beispiel 2 Bit erforderlich:
22 = 4
Beispiel Farben:
Frühere Computer aus den ersten Generationen konnten nur 16 Farben darstellen. Dies lag daran, da für die Speicherung des Farbwertes eines Pixels genau 4 Bit zur Verfügung standen:
24 = 16
Umkehrbeispiel:
Durch Umformen, kann man auch den umgekehrten Fall ermitteln:
Es soll ein Wert gespeichert werden, der 3000 mögliche Werte annehmen kann. Welche Datenmenge ist dafür erforderlich?
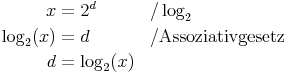
für das konkrete Beispiel gilt somit:
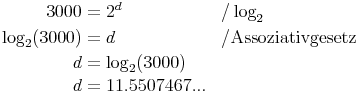
Größere Maßeinheiten
Da die Datenmengen rasant gewachsen sind, haben sich sehr schnell die bekannten Präfixe kilo-, mega-, giga-, tera-, ... etabliert, die zu den Einheiten Kilobyte (Kb), Megabyte (Mb), Gigabyte (Gb), Terabyte (Tb), usw. geführt haben. Für eine Gegenüberstellung aller Maßeinheiten haben wir unter Einheiten für Datenmengen eine entsprechende Übersicht erstellt.
Wichtiger Hinweis zur Umrechnung:
Im Gegensatz zu vielen physikalischen Einheiten, deren Umrechnungszahlen auf Basis des Dezimalsystem beruhen (10, 100, 1000, ...), erfolgen die Umrechnungsschritte hier immer auf Basis von 2. Beispiel:
1 Kilobyte = 28 = 1024 Bytes
Im Abschnitt Umrechnung von Datenmengen haben wir dies nochmals genauer erläutert.
D.h. für die gewünschte Anzahl an Möglichkeiten ist eine Datenmenge von zumindest 12 Bit erforderlich.
Hinweis: die verfügbare Datenmenge ergibt sich immer aus dem aufgerundeten Wert, niemals aus dem abgerundeten Wert. Im oben angeführten Beispiel sieht man:
- 212=4096 Möglichkeiten ... > 3000 ... ist ausreichend
- 211=2048 Möglichkeiten ... < 3000 ... ist nicht ausreichend
Tipp: Falls Sie keine Möglichkeit haben, um den Logarithmus mit Basis 2 zu berechnen, so gibt es eine einfache Formel, mit der von jedem beliebigen Logarithmus auf die Basis 2 umgerechnet werden kann:
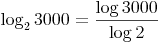
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar