Vektor-Multiplikation

Auf dieser Seite wird die Multiplikation eines Vektors v mit einer Zahl n (skalaren Größe) vorgestellt. Dies entspricht einer n-fachen Verschiebung v.

Abb. 1: Vektormultiplikation

Vektormultiplikation

Multiplikation eines Vektors mit einem Skalar

Wird eine Verschiebung mehrfach hintereinander durchgeführt, kann man diese Verschiebungen mit einer skalaren Multiplikation zusammenfassen.

Beispiel:

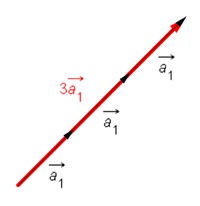
In Abbildung 1 wird eine Verschiebung a₁ drei mal durchgeführt. Die Gesamtverschiebung kann man somit ermitteln mit:

$\vec{a_{ges}}=\vec{a_1}+\vec{a_1}+\vec{a_1}=3\cdot\vec{a_1}$

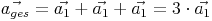
Bei einer Multiplikation eines Vektors mit einer Zahl wird jede Komponente (x, y, ...) mit der Zahl selbst multipliziert:

$c\cdot\vec{v}=c\cdot\left(\begin{array}{r}v_x\\v_y\end{array}\right)=\left(\begin{array}{r}c\cdot{v_x}\\c\cdot{v_y}\end{array}\right)$

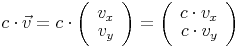
Vektormultiplikation in der Ebene

$5\cdot\left(\begin{array}{r}7\\-2\end{array}\right)=\left(\begin{array}{rrr}5&\cdot&7\\5&\cdot&(-2)\end{array}\right)=\left(\begin{array}{r}35\\-10\end{array}\right)$

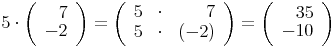
Vektormultiplikation im Raum

$3\cdot\left(\begin{array}{r}4\\0,5\\2\end{array}\right)=\left(\begin{array}{rrr}3&\cdot&4\\3&\cdot&0,5\\3&\cdot&2\end{array}\right)=\left(\begin{array}{r}12\\1,5\\6\end{array}\right)$

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
1,9
98 Bewertungen

Kommentar #41330 von Geheim 27.06.18 13:18 Geheim: NICHT HILFREICH