Zinseszinsen

Hebt man die Zinsen am Jahresende nicht vom Sparbuch ab, so werden sie im nächsten Jahr mitverzinst. Im nächsten Jahr erhält man also Zinsen für das Kapital UND für die Zinsen des 1. Jahres. Man spricht in diesem Fall von Zinseszinsen.

Beispiel:

Herr Unger zahlt 5 000 Euro auf sein Sparbuch ein. Er möchte das Geld erst nach 5 Jahren abheben. Wie groß ist das Guthaben nach 5 Jahren bei einem Zinssatz von 3%?

Die Formel zur Berechnung von Jahreszinsen kennen wir bereits aus einem der vorhergehenden Kapiteln:

Berechnung von Jahreszinsen:

$Z = \frac{K \cdot p} {100}$

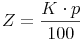
Wir berechnen nun also mit Hilfe dieser Formel die Zinsen für das 1. Jahr: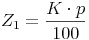

$Z_1 = \frac{K \cdot p}{100}$

$Z_1 = \frac{5\ 000 \cdot 3}{100}$

Z_1 = 150

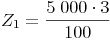
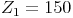
Am Ende des 1. Jahre beträgt das Kapital nun also 5 000 + 150 = 5 150 Euro.

Da die Zinsen am Ende des 1. Jahres nicht abgehoben werden, beträgt das zu verzinsende Kapital am Beginn des 2. Jahres 5 150 Euro: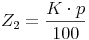

$Z_2 = \frac{K \cdot p}{100}$

$Z_2 = \frac{5\ 150 \cdot 3}{100}$

Z_2 = 154,50

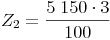
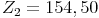
Die Zinsen für das 2. Jahr betragen 154,50 Euro. Addiert man diese nun zum Ausgangskapital des 2. Jahres, so erhält man das Endkapital des 2. Jahres: 5 150 + 154,50 = 5 304,50 Euro.

Analog dazu werden nun die Zinseszinsen für das 3., 4. und 5. Jahr berechnet. Wir beschränken uns nun auf eine Auflistung in der folgenden Tabelle:

Jahr	Kapital am Jahresanfang	Zinssatz	Zinsen	Kapital am Jahresende
1	5 000 €	3%	150	5 150 €
2	5 150 €	3%	154.50	5 304.50 €
3	5 304.50 €	3%	159.14	5 463.64 €
4	5 463.64 €	3%	163.91	5 627.54 €
5	5 627.54 €	3%	168.83	5 796.37 €

Antwort: Ein Kapital von 5 000 Euro ist nach 5 Jahren bei einem Zinssatz von 3% auf 5 796,37 Euro angewachsen.

Herleitung der Formel: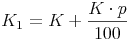

$K_1 = K + \frac{K \cdot p}{100}$

$K_1 = K + \frac{K \cdot 3}{100}$

$K_1 = K + K \cdot 0,03$

$K_1 = K + 0,03 \cdot K$

$K_1 = 1 \cdot K + 0,03 \cdot K$

$K_1 = 1,03 \cdot K$

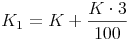
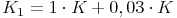
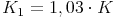
Um das Endkapital am Ende des 1. Jahres zu berechnen, muss also das Anfangskapital des 1. Jahres mit 1,03 multipliziert werden.

Um das Endkapital am Ende des 2. Jahres zu berechnen, muss also das Anfangskapital des 2. Jahres mit 1,03 multipliziert werden.

Um das Endkapital am Ende des 3. Jahres zu berechnen, muss also das Anfangskapital des 3. Jahres mit 1,03 multipliziert werden.

usw.

Wir rechnen: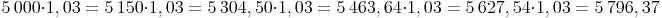

$5\ 000 \cdot 1,03 = 5\ 150 \cdot 1,03 = 5\ 304,50 \cdot 1,03 = 5\ 463,64 \cdot 1,03 = 5\ 627,54 \cdot 1,03 = 5\ 796,37$

Um das Endkapital nach 5 Jahren mit Zinseszinsen zu berechnen, muss also das Startkapital 5 Mal mit 1,03 multipliziert werden: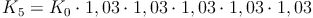

$K_5 = K_0 \cdot 1,03 \cdot 1,03 \cdot 1,03 \cdot 1,03 \cdot 1,03$

$K_5 = K_0 \cdot 1,03^5$

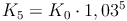
Allgemein ergibt sich bei einem Zinssatz von 3 Prozent in n Jahren folgende Formel: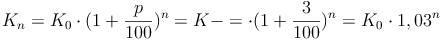

$K_n = K_0 \cdot (1 + \frac{p}{100})^n = K-= \cdot (1 + \frac{3}{100})^n = K_0 \cdot 1,03^n$

Berechnung von Zinseszinsen:

Hebt man die Zinsen am Jahresende nicht vom Sparbuch ab, so werden sie im nächsten Jahr mitverzinst. Im nächsten Jahr erhält man also Zinsen für das Kapital UND für die Zinsen des 1. Jahres. Man spricht in diesem Fall von Zinseszinsen.

$K_n = K_0 \cdot (1+ \frac{p}{100})^n$

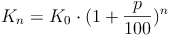
Beispiel:
Anfangskapital K_0

und Zinssatz 4% nach 5 Jahren:
$K_5 = K_0 \cdot (1+ \frac{4}{100})^5 = K_0 \cdot 1,04^5$

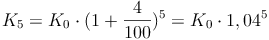
Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,6
111 Bewertungen

Kommentar #40200 von Less 03.10.17 20:42 Less: hat mir sehr geholfen. Danke
Kommentar #40970 von Luftverbraucher 09.04.18 13:17 Luftverbraucher: gut erklärt. ist leicht zu verstehen.

Zinseszinsen

Zinseszinsen

Kommentar verfassen

Ähnliche Arbeitsblätter