Bei der zentrischen Streckung wird eine ebene Figur von einem Streckungszentrum aus vergrößert.
Beispiel:
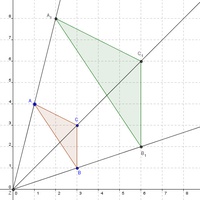
In unserem Beispiel wurde ein Dreieck mit den Koordinaten A (1 / 4), B (3 / 1 ) und C (3 / 3) durch zentrische Streckung um das doppelte (2fache) vergrößert. Als Streckungszentrum wurde der Ursprung des Koordinatensystems (0 / 0) gewählt. Der Streckungsfaktor k = 2.
Die Koordinaten des so entstandenen Dreicks lauten 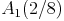 ,
, 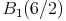 und
und 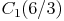 .
.
Die beiden Dreieck sind zueinander ähnlich: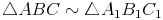
Es gilt:
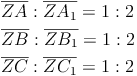
Es gilt auch:
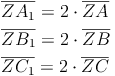
Die Seiten der vergrößerten Figur sind parallel zu den Seiten der ursprünglichen Figur:
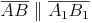
Zentrische Streckung von ebenen Figuren:
Eine zentrische Streckung erfolgt aus dem Streckungszentrum Z mit dem Streckungsfaktor k.
Es gilt:
- Ein Punkt X und sein Bildpunkt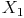 liegen auf einem gemeinsamen Strahl, der von Z ausgeht
liegen auf einem gemeinsamen Strahl, der von Z ausgeht
- Jeder Bildpunkt ist vom Streckungszentrum k-Mal so weit entfernt wie der ursprüngliche Punkt.
- die Seiten der vergrößerten Figur verlaufen parallel zu den entsprechenden Seiten der ursprünglichen Figur
Eine zentrische Streckung erfolgt aus dem Streckungszentrum Z mit dem Streckungsfaktor k.
Es gilt:
- Ein Punkt X und sein Bildpunkt
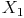 liegen auf einem gemeinsamen Strahl, der von Z ausgeht
liegen auf einem gemeinsamen Strahl, der von Z ausgeht- Jeder Bildpunkt ist vom Streckungszentrum k-Mal so weit entfernt wie der ursprüngliche Punkt.
- die Seiten der vergrößerten Figur verlaufen parallel zu den entsprechenden Seiten der ursprünglichen Figur
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Christoph Pirnbacher
Warum ist das Verhältnis ZA : ZA_1 = 1 : 3 wenn wir einen Streckungsfaktor von k = 2 haben?
Erich Hnilica, BEd
Danke für die Info!
Den Fehler haben wir bereits behoben.