Das Streckungszentrum liegt außerhalb der Figur

Auf dieser Seite möchten wir Ihnen zeigen, wie Sie eine ebene Figur um einen Streckungsfaktor k vergrößern können, wenn das Streckungszentrum Z außerhalb der ebenen Figur liegt.
Streckung 1 Streckung 1
Streckung 2 Streckung 2
Streckung 3 Streckung 3
Streckung 4 Streckung 4

Auf dieser Seite möchten wir Ihnen zeigen, wie Sie eine ebene Figur um einen Streckungsfaktor k vergrößern können, wenn das Streckungszentrum Z außerhalb der ebenen Figur liegt.


Beispiel:

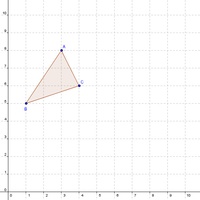
Konstruieren Sie das Dreieck ABC, dessen Eckpunkte folgende Koordinaten aufweisen: A (3 / 8), B (1 / 5) und C (4 / 6).

Schritt 1:

Konstruieren Sie die Punkte A, B und C in einem rechtwinkeligen Koordinatensystem und verbinden Sie diese zu einem Dreieck.

Schritt 2:

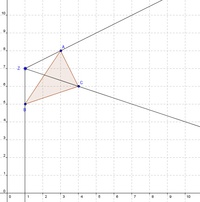
Konstruieren Sie das Streckungszentrum Z und zeichnen Sie von diesem Punkt aus jeweils einen Strahl durch die Eckpunkte des Dreiecks.

Vergrößern Sie anschließend dieses Dreieck vom Streckungszentrum Z (1 / 7) aus, wobei der Eckpunkt 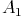A_1 des vergrößerten Dreiecks bereits bekannt ist: A_1 (7/10).

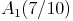Schritt 3:

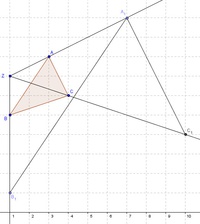
Konstruieren Sie nun den Eckpunkt 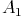A_1 des vergrößerten Dreiecks. Da die Seiten des vergrößerten Dreiecks zu jenen des ursprünglichen Dreiecks parallel verlaufen, können Sie nun die Seiten des ursprünglichen Dreiecks parallel verschieben.

(Verschieben Sie die Seite AB parallel durch den Punkt 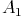A_1, dann die Seite AC parallel durch den Punkt 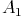A_1. Dort wo die beiden Parallelen die Strahlen schneiden befinden sich die Eckpunkte B_1\ \text{und}\ C_1).

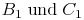Schritt 4:

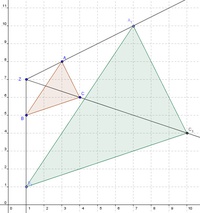
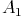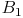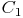Abschließend müssen Sie nur noch die Eckpunkte A_1, B_1 und C_1 miteinander verbinden.

Das Streckungszentrum liegt außerhalb der Figur

Liegt das Streckungszentrum Z außerhalb der ursprünglichen Figur, so können die beiden Figuren einander schneiden, müssen jedoch nicht.

Kommentar verfassen