Das Streckungszentrum liegt in einem Eckpunkt der Figur

Auf dieser Seite möchten wir Ihnen zeigen, wie Sie eine ebene Figur um einen Streckungsfaktor k vergrößern können, wenn das Streckungszentrum Zin einem Eckpunkt der Figur liegt.
Streckung 1 Streckung 1
Streckung 2 Streckung 2
Streckung 3 Streckung 3
Streckung 4 Streckung 4

Auf dieser Seite möchten wir Ihnen zeigen, wie Sie eine ebene Figur um einen Streckungsfaktor k vergrößern können, wenn das Streckungszentrum Z mit einem Eckpunkt der ebenen Figur zusammenfällt.

Beispiel:

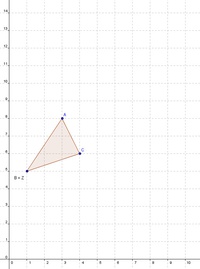
Konstruieren Sie das Dreieck ABC, dessen Eckpunkte folgende Koordinaten aufweisen: A (3 / 8), B (1 / 5) und C (4 / 6).

Vergrößern Sie anschließend dieses Dreieck vom Streckungszentrum Z aus, wobei die Koordinaten von Z identisch sind mit jenen des Eckpunktes B. Außerdem ist der Eckpunkt 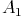A_1 des vergrößerten Dreiecks bereits bekannt: A_1 (7/10).


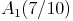Schritt 1:

Konstruieren Sie die Punkte A, B und C in einem rechtwinkeligen Koordinatensystem und verbinden Sie diese zu einem Dreieck.

Schritt 2:

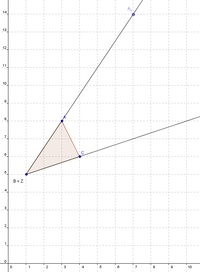
Zeichnen Sie das Streckungszentrum Z im Eckpunkt B ein und zeichnen Sie von diesem Punkt aus jeweils einen Strahl durch die Eckpunkte des Dreiecks. (verlängern Sie also die Seiten BA und BC des Dreiecks)

Schritt 3:

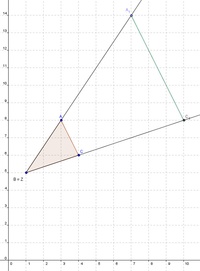
Konstruieren Sie nun den Eckpunkt A_1. Dieser liegt auf dem Strahl, der durch die Eckpunkte B und A verläuft.

Verschieben Sie die Seite AC parallel durch den Punkt 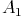A_1, der Schnittpunkt dieser Geraden mit dem anderen Strahl führt zum Eckpunkt C_1.

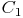Schritt 4:

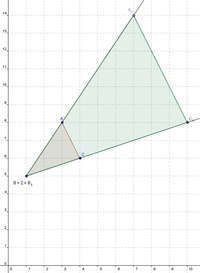
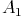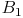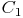Abschließend müssen Sie nur noch die Eckpunkte A_1, B_1 und C_1 miteinander verbinden.

Lösungen: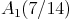

A_1 ( 7 / 14)
B_1 (1 / 5)
C_1 (10 / 8)

Das Streckungszentrum liegt in einem Eckpunkt der Figur

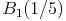
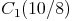
Liegt das Streckungszentrum Z in einem Eckpunkt der ursprünglichen Figur, so liegen zwei Seiten der beiden Figuren übereinander. Zwei Seiten der ursprünglichen Figur sind also ein Teilstück der jeweiligen Seiten der vergrößerten Figur.

Kommentar verfassen