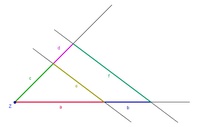
Konstruieren Sie zwei beliebige Strahlen vom gemeinsamen Anfangspunkt Z aus.
Wenn Sie diese beiden Strahlen mit zwei parallelen Geraden schneiden, erhalten Sie die typische Strahlensatzfigur.
1. Erkenntnis:
Durch die Ähnlichkeit der Dreiecke 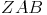 und
und 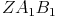 gilt:
gilt:
Die Abschnitte auf den beiden Strahlen stehen im gleichen Verhältnis zueinander.
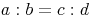
[sprich: a zu b verhält sich gleich wie c zu d]
Als Bruch geschrieben: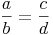
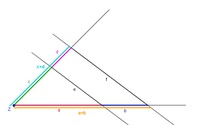
2. Erkenntnis:
Ebenso gilt: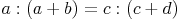
Als Bruch geschrieben: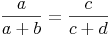
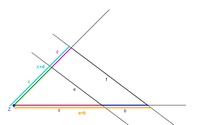
3. Erkenntnis:
Ebenso gilt: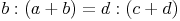
Als Bruch geschrieben: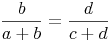
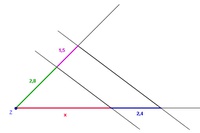
Anwendungsbeispiel:
Berechnen Sie die fehlende Länge!
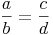
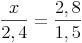
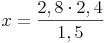
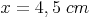
1. Strahlensatz:
Die Abschnitte des ersten Strahles verhalten sich wie die entsprechenden Abschnitte auf dem zweiten Strahl.
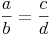

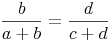
Die Abschnitte des ersten Strahles verhalten sich wie die entsprechenden Abschnitte auf dem zweiten Strahl.
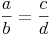

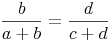
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar