Proportionale Strecken

Mit Hilfe der Strahlensätze lässt sich eine Streckenlänge berechnen bzw. konstruktiv ermitteln, wenn zwei Strecken in einem bestimmten Verhältnis zueinander stehen und die Länge einer Strecke bekannt ist.

Hier möchten wir Ihnen demonstrieren, wie Sie mit Hilfe der Strahlensätze Streckenlängen berechnen bzw. konstruktiv erarbeiten können, wenn zwei Strecken in einem bestimmten Verhältnis zueinander stehen und die Länge einer Strecke bekannt ist.


Beispiel:

Ermitteln Sie die Länge der Strecke b, wenn Sie die Länge der Strecke a kennen (a = 6 cm) und die beiden Strecken im Verhältnis 3 : 4 zueinander stehen.

a : b = 3 : 4

wobei a = 6 cm

1. rechnerischer Lösungsweg: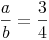

\frac{a}{b} = \frac{3}{4}

\frac{6}{b} = \frac{3}{4}\quad / \cdot b

6 = \frac{3 \cdot b}{4}\quad / \cdot 4

6 \cdot 4 = 3 \cdot b

24 = 3 \cdot b\quad / : 3

8 = b

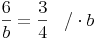
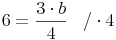
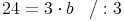
Lösung: b = 8 cm

Proportionale Strecken (Schritt 1) Proportionale Strecken (Schritt 1)
Proportionale Strecken (Schritt 2) Proportionale Strecken (Schritt 2)
Proportionale Strecken (Schritt 3) Proportionale Strecken (Schritt 3)
Proportionale Strecken (Schritt 4) Proportionale Strecken (Schritt 4)

2. konstruktiver Lösungsweg:

Schritt 1:

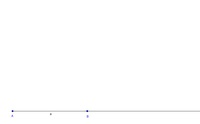
Konstruieren Sie einen waagrechten Strahl.

Zeichnen Sie nun auf diesem Strahl die Strecke a = 6 cm vom Anfangspunkt A aus ein.

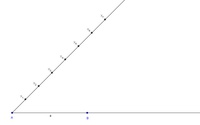
Schritt 2:

Konstruieren Sie einen weiteren Strahl im beliebigen Winkel zum ersten Strahl, allderings mit demselben Anfangspunkt A.

Das Verhältnis beträgt 3 : 4, insgesamt also 3 + 4 = 7 Teile. Daher gilt: Markieren Sie auf dem zweiten Strahl 7 Mal einen beliebig langen Abschnitt. Nehmen Sie dazu einen beliebigen Abstand in den Zirkel und schlagen ihn der Reihe nach 7 Mal hintereinander ab. (Um die Übersicht zu bewahren, beschriften Sie diese Punkte mit 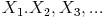X_1. X_2, X_3, ...

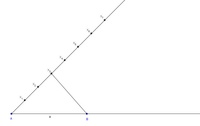
Schritt 3:

Da sich a zu b wie 3 zu 4 verhält, verbinden Sie nun den dritten Punkt 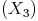(X_3) mit dem Endpunkt der Strecke a.

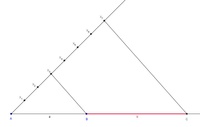
Schritt 4:

Konstruieren Sie nun eine parallele Gerade zu der in Schtt 3 konstruierten Strecke, welche durch den Punkt 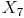X_7 verlaufen soll.

Dort wo die parallele Gerade den 1. Strahl schneidet, markieren wir den Punkt C.

Der Abstand zwischen den Punkten B und C ist nun die Strecke b, welche 8 cm lang ist.

Proportionale Strecken

Mit Hilfe der Strahlensätze lässt sich eine Streckenlänge berechnen bzw. konstruktiv ermitteln, wenn zwei Strecken in einem bestimmten Verhältnis zueinander stehen und die Länge einer Strecke bekannt ist.

Kommentar verfassen