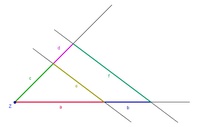
Konstruieren Sie zwei beliebige Strahlen vom gemeinsamen Anfangspunkt Z aus.
Wenn Sie diese beiden Strahlen mit zwei parallelen Geraden schneiden, erhalten Sie die typische Strahlensatzfigur.
1. Erkenntnis:
Durch die Ähnlichkeit der Dreiecke 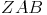 und
und 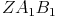 gilt:
Die beiden parallelen Strecken verhalten sich so wie die beiden Abschnitte vom Anfangspunkt A aus auf einem Strahl.
gilt:
Die beiden parallelen Strecken verhalten sich so wie die beiden Abschnitte vom Anfangspunkt A aus auf einem Strahl.
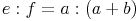
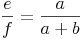
[sprich: e zu f verhält sich gleich wie a zu (a+b)]
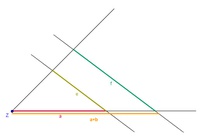
2. Erkenntnis:
Durch diese Ähnlichkeit gilt dies natürlich ebenso für den zweiten Strahl: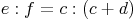
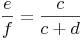
[sprich: e zu f verhält sich gleich wie c zu (c+d)]
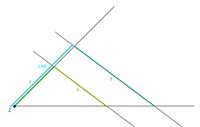
Anwendungsbeispiel:
Berechnen Sie die Höhe des Hauses (x) in der nebenstehenden Skizze!
(Verwenden Sie dazu den 2. Strahlensatz!)
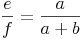

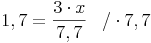
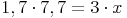
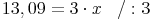
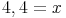
A.: Das Haus ist ca. 4,4m hoch.
Die beiden parallelen Strecken verhalten sich so wie die beiden Abschnitte vom Anfangspunkt A aus auf einem Strahl.
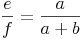
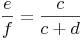
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar

Gusi
Doofe Frage, aber was wenn ich bei der Formel e:f=a:(a+b) a suche? Ich komm nicht auf den Lösungsweg, immer a=0...