Diagonalen in regelmäßigen Vielecken
Dieses Kapitel widmet sich der Anzahl und Länge von Diagonalen von regelmäßigen Vielecken sowie der rechnerischen Ermittlung der Anzahl dieses Diagonalen.
Anzahl der Diagonalen:
Unter einer Diagonale versteht man in der ebenen Geometrie die Verbindungsstrecke von nicht benachbarten Eckpunkten.
Somit besitzen Vielecke je nach Anzahl der Eckpunkte unterschiedlich viele Diagonalen.
Bei einem Dreieck gibt es nur nebeneinanderliegende Eckpunkte, daher besitzt diese geometrische Fläche keine Diagonalen.
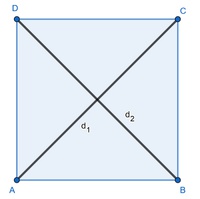
In einem Viereck lassen sich jeweils 2 gegenüberliegende Eckpunkte miteinander verbinden; somit hat ein Viereck zwei Diagonalen.
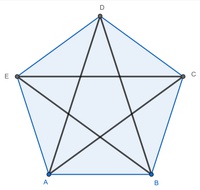
Betrachtet man ein Fünfeck, so kann man erkennen, dass die Anzahl der Diagonalen exponential ansteigt, denn hier können schon fünf Diagonalen eingezeichnet werden.
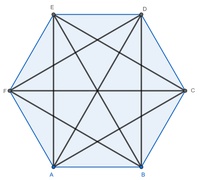
In einem Sechseck lassen sich neun Diagonalen einzeichnen usw.
Länge der Diagonalen:
Die Diagonalen eines regelmäßigen Vierecks und regelmäßigen Fünfecks sind jeweils gleich lang.
Für Vielecke mit mehr als fünf Eckpunkten gilt diese Erkenntnis nicht! Hier haben die Diagonalen unterschiedliche Längen.
Anzahl der Diagonalen berechnen:
Die Anzahl der Diagonalen eines (regelmäßigen) Vielecks mit n Ecken lässt sich mit Hilfe der folgenden Formel rechnerisch ermitteln:
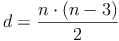
Somit ergibt sich folgende Anzahl an Diagonalen für Vielecke:
| n Ecken | d Diagonalen |
|---|---|
| 3 | 0 |
| 4 | 2 |
| 5 | 5 |
| 6 | 9 |
| 7 | 14 |
| 8 | 20 |
| 9 | 27 |
| 10 | 35 |
| 11 | 44 |
| 12 | 54 |
| 13 | 65 |
| 14 | 77 |
| 15 | 90 |
Unter Diagonalen versteht man in der ebenen Geometrie Verbindungsstrecken von nicht benachbarten Eckpunkten.
Die Anzahl der Diagonalen eines (regelmäßigen) Vielecks mit n Ecken lässt sich mit Hilfe der folgenden Formel rechnerisch ermitteln:
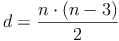
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar