Kanten

Ein dreiseitiges Prisma hat insgesamt 9 Kanten. Jeweils 2 Kanten der Grund- und Deckfläche sind parallel und gleich lang. Zudem sind die 3 Höhen parallel und gleich lang.

Die Kanten des dreiseitigen Prismas

In den Kanten treffen jeweils 2 Seitenflächen des dreiseitigen Prismas aufeinander.

Eine Kante verbindet 2 Eckpunkte miteinander.

Ein dreiseitiges Prisma hat insgesamt 9 Kanten, die allerdings nicht alle gleich lang sind.

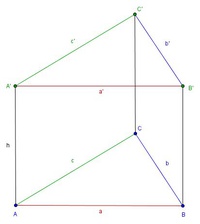
Da die Dreiecke der Grund- und Deckfläche kongruent sind, sind auch jeweils die 3 Dreiecksseiten der Grund- und Deckfläche parallel und gleich lang:

a = a_1 \text{ , } b = b_1 \text{ , } c = c_1

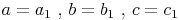
Zudem sind die 3 Höhen des dreiseitigen Prismas ebenfalls parallel und gleich lang.

Die Beschriftung der Kanten erfolgt mit für Strecken üblichen Kleinbuchstaben.

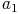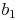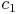Üblicherweise werden die ersten Buchstaben des Alphabets (a, b und c) zur Beschriftung der Grundfläche verwendet, die Deckfläche mit a_1, b_1 und c_1. Für die Höhe wird oft ein h zur Beschriftung herangezogen.

Das dreiseitige Prisma:

Ein dreiseitiges Prisma hat insgesamt 9 Kanten.
Jeweils 2 Kanten der Grund- und Deckfläche sind parallel und gleich lang. Zudem sind die 3 Höhen parallel und gleich lang.
Kommentar #42896 von svynt 15.09.19 20:15
svynt

danke für die hilfe

Kommentar verfassen