mit ungleichnamigen Brüchen

Addieren und Subtrahieren von Brüchen mit unterschiedlichen Nennern

Addieren und Subtrahieren ungleichnamiger Brüche

Brüche, die unterschiedliche Nenner haben, bezeichnet man als ungleichnamige Brüche.

z.B. \frac {4}{9}, \frac{3}{8}

Eine Familie bestellt 3 Pizzen. Stefan bekommt

- von der 1. Pizza ein Viertel 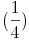(\frac {1}{4})

- von der 2. Pizza die Hälfte 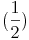(\frac {1}{2})

- von der 3. Pizza ein Achtel 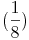(\frac {1}{8})

Wie viel Pizza hat er gegessen?

Um die Aufgabe lösen zu können, müssen die Pizzen in gleiche Teile geteilt werden (die Brüche auf denselben Nenner gebracht werden)

Dazu ermittelt man das kleinste gemeinsame Vielfache (kgV) der Nenner (also der Zahlen 4, 2, 8):

Vielfache von 4: 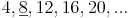4, \underline{8}, 12, 16, 20, ...

Vielfache von 2: 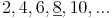2, 4, 6, \underline{8}, 10, ...

Vielfache von 8: 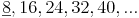\underline{8}, 16, 24, 32, 40, ...

Das kleinste gemeinsame Vielfache ist 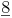\underline{8}!

Der erste Bruch ist mit 2 zu erweitern (zu multiplizieren), weil das kleinste gemeinsame Vielfache an 2. Stelle steht.

Der 2. Bruch mit 4, der 3. Bruch mit 1!

1. Pizza: 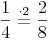\frac {1}{4} \stackrel{\mathrm{\cdot 2}}= \frac {2}{8}

2. Pizza: 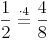\frac {1}{2} \stackrel{\mathrm{\cdot 4}}= \frac {4}{8}

3. Pizza: 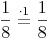\frac {1}{8} \stackrel{\mathrm{\cdot 1}}= \frac {1}{8}

Gesamt: 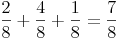\frac {2}{8} + \frac {4}{8} + \frac {1}{8} = \frac {7}{8}

Um ungleichnamige Brüche addieren (bzw. subtrahieren) zu können, müssen die Brüche zuerst gleichnamig gemacht werden (auf den gleichen Nenner bringen).

Dazu ermittelt man den kleinsten gemeinsamen Nenner (= das kgV der Nenner ermitteln).

Anschließend werden die Zähler addiert (bzw. subtrahiert) und der Nenner unverändert gelassen.

Weiteres Beispiel:

\frac {3}{4} - \frac {2}{5} =

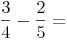
Vielfache des 1. Nenners: 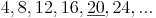4, 8, 12, 16, \underline{20}, 24, ...

Vielfache des 2. Nenners: 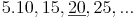5. 10, 15, \underline{20}, 25, ...

Kleinster gemeinsamer Nenner: 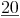\underline{20}

Der erste Bruch ist mit 5 zu erweitern (zu multiplizieren), weil das kleinste gemeinsame Vielfache an 5. Stelle steht.

Der 2. Bruch ist mit 4 zu erweitern!

\frac {3}{4} - \frac {2}{5} = \frac {15}{20} - \frac {8}{20} = \frac {7}{20}

Kommentar #15 von Benjamin 22.11.10 20:48
Benjamin

Was ist den mit den Zahlen 5, 11 und 3. Welche Zahl haben diese drei Werte gemeinsam

Kommentar #16 von Admin 22.11.10 21:09
Admin

Ich nehme an, du meinst drei Brüche mit den Nennern 5, 11 und 3. In dem Fall wird der kleinste gemeinsame Nenner etwas größer, da es sich bei allen drei Zahlen um Primzahlen handelt. Der gemeinsame Nenner ist dann somit 5 * 11 * 3 = 165

Den Zähler von .../5 musst du dann mit (11 * 3) multiplizieren
Den Zähler von .../11 musst du mit (3 * 5) multiplizieren
Den Zähler von .../3 musst du mit (5 * 11) multiplizieren

Beispiel:

2/5 + 1/3 + 3/11 = 66/165 + 55/165 + 45/165 = 166/165 oder 1 Ganzes 1/165

Kommentar #355 von ali 14.02.11 18:40
ali

ungleichnamige brüche subtrahieren . berechne das ergebniss als gemischte zahl

Kommentar #453 von Sila 14.08.11 11:14
Sila

Hallo ! Ich habe für morgen eine Hausaufgabe in Mathematik auf bekommen .. Das Thema ist Ungleichnamige Brüche - größer , kleiner oder gleich... Ich kenne die Zeichen dazu schon aber die Rechnug ... !! Ich weis es überhaupt nicht , wie ich es machen soll .. Könnt ihr mir BITTE helfen ?! :) Das währe toll.. Ich Danke ! Sila

Kommentar #535 von Alica Räth 16.12.11 17:43
Alica Räth

Hallo ich habe eine Frage was ist wenn man keine gemeinsame Vielfachzahl findet ?

Kommentar #8518 von Sophie 09.02.14 18:26
Sophie

Ich habe hier eine aufgabe wo noch eine Zahl vor dem Bruch steht. gibt es dafür auch noch erklärung?

Kommentar #9308 von kamal 14.10.14 18:06
kamal

wie geht das erweitern von ungleichnamigen zahlen

Kommentar #9864 von Erich Hnilica, BEd 04.04.15 12:20
Erich Hnilica, BEd

Hallo Kamal!

Dazu gibt es ein eigenes Kapitel - dort wird dir alles genau erklärt.

Kommentar #13134 von Verstehe das nicht ganz ^*^ 01.03.16 17:30
Verstehe das nicht ganz ^*^

Verstehe es nicht ganz :-

Kommentar verfassen