Division eines Bruches durch einen Bruch
Beispiel:
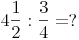
1. Falls nötig in unechte Brüche umwandeln: 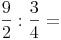
2. Den Kehrwert des 2. Bruches und das Divisionszeichen durch ein Malzeichen ersetzen: 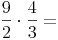
Unter dem Kehrwert (reziproken Wert) eines Bruches versteht man das Vertauschen von Zähler und Nenner.
3. Falls möglich, wird jetzt gekürzt (in unserem Beispiel 2 und 4 sowie 3 und 9): 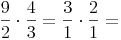
4. Ausführen der Multiplikation: 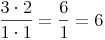
Man dividiert einen Bruch durch einen anderen Bruch, indem man den 1. Bruch mit dem Kehrwert des 2. Bruches multipliziert.
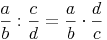
Beispiel: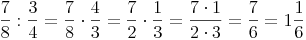
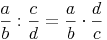
Beispiel:
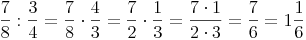
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Noah
Ich hatte das mit dem Kehrwert im Unterricht nicht so richtig verstanden, und wir schreiben morgen einen Test.
Vielen Dank mathe-lexikon.at